Реферат: Экзаменационные билеты по математике
Билет № 9
-
Формула угла между прямыми на плоскости, заданными своими угловыми уравнениями. Условие параллельности и перпендикулярности прямых на плоскости.
-
Что такое стохастический (случайный) эксперимент, событие, элементарные события? Привести пример случайного эксперимента и описать в нем элементарные события.
-
Определить, какие из точек К (0, -4), L (-1,1), M (6, -9) принадлежат множеству
А = {(x,y) : x2 + 1 ≥ y ≥ -x -3}. -
Найти длину вектора
 – 3
– 3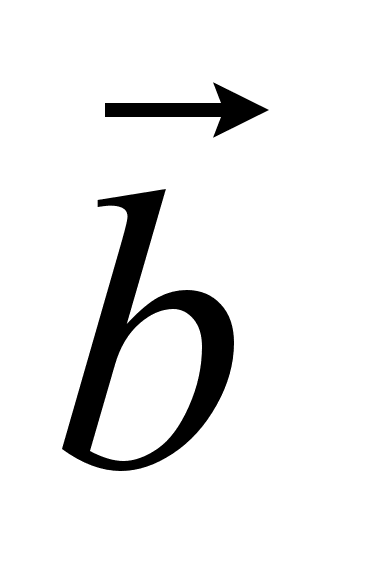 , если дано:
, если дано:  {2, -4, -1},
{2, -4, -1}, 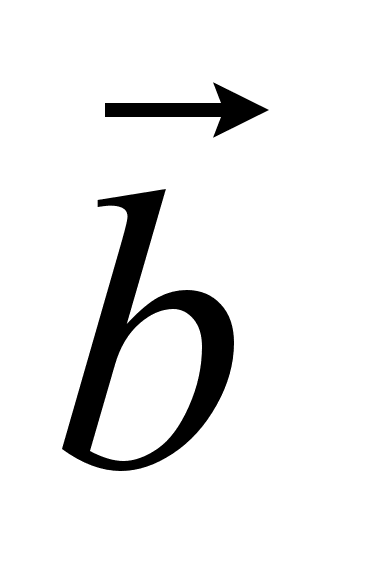 {-1, -3, 1}.
{-1, -3, 1}. -
Найти интервалы монотонности функции ƒ(х) = х4 – 2х2 –3.
-
Случайная величина X задана рядом распределения:

найти Р3 и DX.
Зав. кафедрой
--------------------------------------------------
Экзаменационный билет по предмету
МАТЕМАТИКА. БАЗОВЫЙ КУРС (ДЛЯ ЭКОНОМИСТОВ И МЕНЕДЖЕРОВ)
Билет № 10
-
Дать определение области определения и области значений числовой функции. Описать области определения и значений функции y =
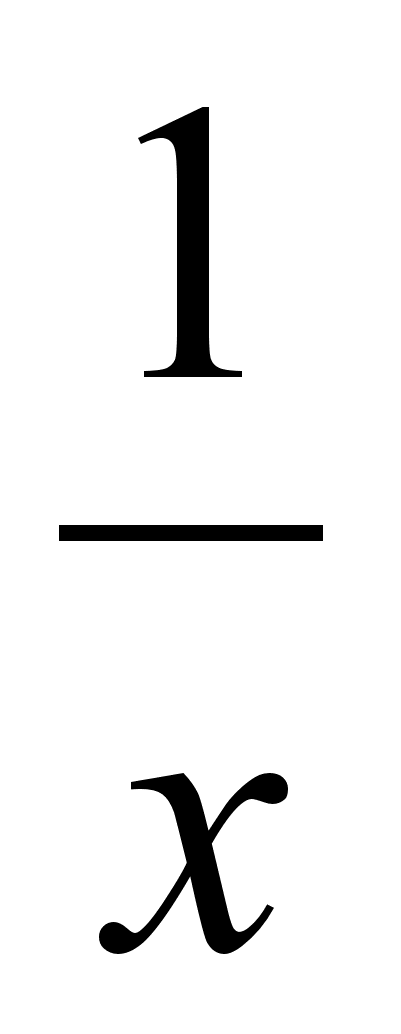 .
. -
Что такое схема Бернулли? Записать асимптотические формулы Муавра-Лапласа и объяснить, при каких условиях они применяются.
-
Даны числовые множества: А = {3х | x целое}, В = {х2 | х целое}, С= (-2, 12). Найти
(А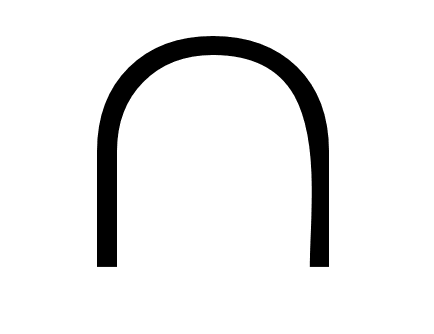 С) \ В.
С) \ В. -
Найти общее уравнение высоты треугольника АВС из точки А, если известно:
А (-1, 4), В (-1, 0), С (2, 1). -
Найти производную функции f(x) =
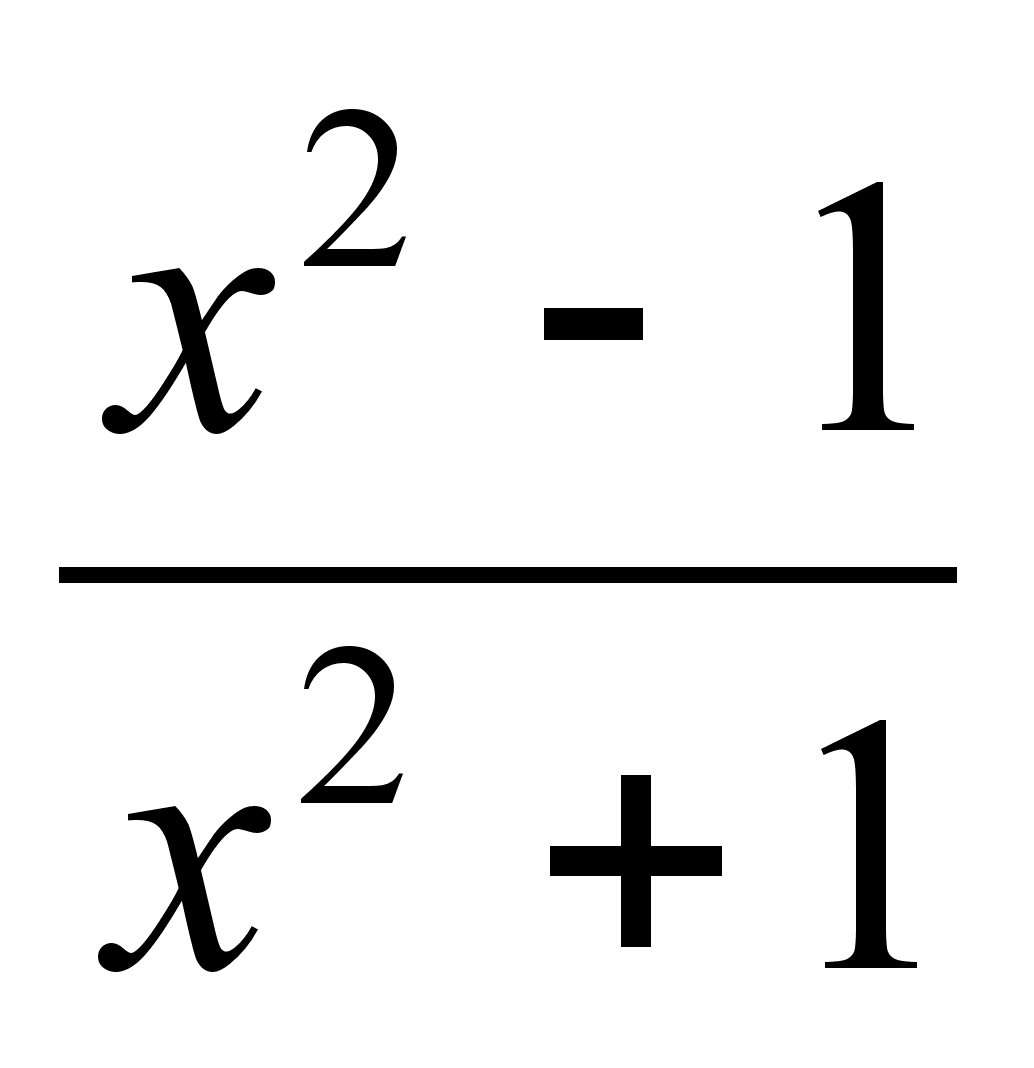 .
. -
Вероятность того, что денежная купюра фальшивая равна 0.001. Найти вероятность того, что среди 500 полученных Вами купюр имеется фальшивая.
Зав. кафедрой
--------------------------------------------------
Экзаменационный билет по предмету
МАТЕМАТИКА. БАЗОВЫЙ КУРС (ДЛЯ ЭКОНОМИСТОВ И МЕНЕДЖЕРОВ)
Билет № 11
-
Каноническое уравнение гиперболы. Геометрический смысл его параметров. Формулы координат фокусов. Привести пример.
-
Дать определение независимых событий. Записать формулу вероятности произведения независимых событий и привести пример ее применения.
-
Найти сумму первых 5 членов геометрической прогрессии, если первый член равен 3, а четвертый -24.
-
Написать уравнение плоскости, походящей через точку А(1,0,-1) параллельно плоскости 4x + 2y - 5z - 4 = 0.
-
Вычислить неопределенный интеграл
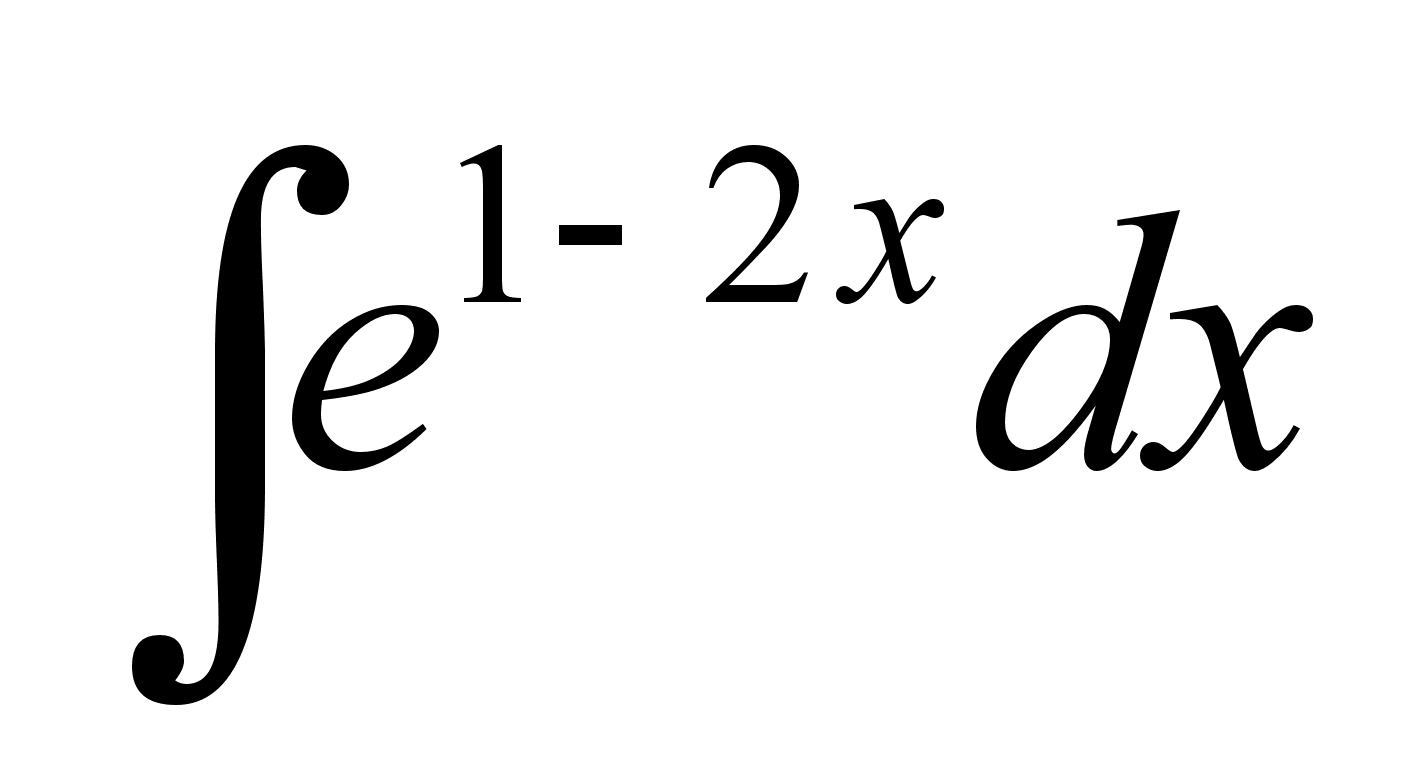 .
. -
Рабочий обслуживает три станка. Вероятность того, что в течение часа станок не потребует внимания рабочего равна: для первого станка 0,9, для второго 0,8, для третьего - 0,85. Какова вероятность того , что в течение некоторого часа, по крайней мере, один станок потребует внимания?