Реферат: Геометрия физического пространства
4.3.6.1*. – x2 – y2 – z2 + t2 – e2 +1 = 0.
Используя законы тригонометрии уравнения 4.3.6.1 и 4.3.6.1* раскладываются на множители следующим образом:
– sh2 α · cos2 β · cos2 γ – sh2 α · cos2 β · sin2 γ – sh2 α · sin2 β + ch2 α · cos2 δ + ch2 α · sin2 δ – 1 = 0.
4.3.6.2*. – ch2 α · cos2 β · cos2 γ – ch2 α · cos2 β · sin2 γ – ch2 α · sin2 β · cos2 δ + sh2 α – ch2 α · sin2 β sin2 δ + 1 = 0.
4.3.7. Фотон:
2.1.3.5. (X1)2 – (X2)2 – (X3)2 + (X4)2 + (X5)2 = 0 преобразовывается:
4.3.7.1. – x2 – y2 + t2 + e2 – 1 = 0.
4.3.7.1*. – x2 – y2 + t2 – e2 +1 = 0.
Тригонометрическое преобразование уравнений 4.3.7.1 и 4.3.7.1* приводит к следующему:
4.3.7.2. – sh2 α · cos2 β – sh2 α · sin2 β + ch2 α · cos2 δ + ch2 α · sin2 δ – 1 = 0
4.3.7.2*. – ch2 α · cos2 β · cos2 γ – ch2 α · cos2 β · sin2 γ – ch2 α · sin2 β + sh2 α + 1 = 0
Уравнение 4.3.7.2 получается из уравнения 4.3.6.2 при условии γ = πn/2, а уравнение 4.3.7.2* из уравнения 4.3.6.2* при условии δ = πn/2. Уравнение 2.1.3.5 имеет SU(2, 3)-группу вращения.
4.3.8. Глюон:
2.1.3.3. (X1)2 – (X2)2 – (X3)2 + (X4)2 = 0 можно преобразовать:
4.3.8.1. – x2 + t2 + e2 – 1 = 0
4.3.8.1*. – x2 + t2 – e2 +1 = 0
4.3.8.2. – sh2 α + ch2 α · cos2 δ + ch2 α · sin2 δ – 1 = 0
4.3.8.2*. – ch2 α · cos2 β – ch2 α · sin2 β + sh2 α + 1 = 0
Уравнение 4.3.8.2 преобразуется из уравнения 4.1.1 при условии β = πn/2; γ = πn/2, а уравнение 4.3.8.2* из уравнения 4.1.1* при условии γ = πn/2; δ = πn/2. Уравнения 2.1.3.3 имеют SU(2, 2)-группу вращения.
4.4. Особенности подпространств
Хотя каждое из подпространств физического пространства, в соответствии с аксиомой 1.2, не является особым, выделенным, но одновременно и не идентичным другим. Каждое из подпространств имеет свои особенности, которые мы и рассмотрим.
4.4.1. Гравитон
Важнейшей особенностью гравитационного поля является то, что оно является пространство-образующим. Оно определяет размерность наблюдаемого физического пространства (–1; 1; 1; 1), а все другие поля действуют в пространстве гравитационного поля. Нет для гравитации пространства (поля), внешнего по отношению к нему. Нельзя оказаться внешним по отношению к гравитационному полю. А потому любое наблюдаемое гравитационное взаимодействие есть остаточное взаимодействие внутри гравитонного потока сил типа Вандерваальсовских, а, следовательно, гравитационное взаимодействие материальных тел должно быть весьма слабым, что и наблюдается.
Другой отличительной особенностью является то, что локально «пустое» пространство обладает антигравитационным эффектом, экспоненциально растущим с ростом расстояния. Об этом свидетельствуют решения уравнений Эйнштейна для «пустого» пространства.
Это же можно достаточно наглядно продемонстрировать геометрически. Если кому-либо не нравится термин – антигравитация – то разговор можно вести в геометрических понятиях пространств отрицательной, положительной или нулевой кривизны. Суть не изменится (напоминаем об аксиоме 1.3).
Понятие «пустого» пространства подразумевает отсутствие в нем сколько-нибудь значимых масс,
зарядов, электромагнитных и прочих полей. Поместим в него тела отсчета и пробное, не способные ощутимо исказить геометрию пространства. Для свободной системы тел проекции их мировых линий в любом евклидовом сечении физического пространства будут, в общем случае, прямыми линиями. Поэтому интерес представляют гиперболические сечения (плоскости Минковского), см. рис.1.
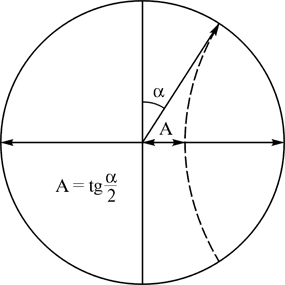
Рис. 1. Мировые линии тел отсчета и пробного в «пустом» пространстве.