Реферат: Геометрия физического пространства

что происходит при их аннигиляции?

причем здесь слабые фермионы?

и где же эти вездесущие нейтрино?

Последним вообще как бы не остается места при выше принятой классификации полей. Поиск ответов приводит к смене знаков базиса.

Нет никакого принципиального геометрического (и физического) запрета к смене знаков базиса физического пространства (умножении векторов базиса на –1). Поменяв знаки базиса на противоположные получим комплексное под пространство, сопряженное первому.

В этом случае все становится на место. В сопряженном физическом подпространстве мировые линии частиц (примем для них общее название – «нейтрино») будут располагаться в нашей системе координат согласно рис.3.

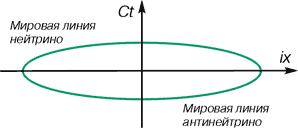
Рис. 3. Мировые линии нейтрино

Смена знаков в уравнениях 2.1.3.1...2.1.3.7 существенно изменит свойства большинства из них, кроме уравнений 2.1.3.1,о котором речь пойдет ниже, и уравнения 2.1.3.2.

В уравнении 2.1.3.2 смена знаков приведет к следующему:

(X1)² – (X2)² + (X3)² = 0 при смене знаков получим:

2.1.3.2*. – (X1)² + (X2)² – (X3)² = 0 или

x² – e² + 1 = 0

2.1.3.2.1*. – x² + e² – 1 = 0

По сравнению с уравнениями:

– x² + e² – 1 = 0

4.3.5.1*. x² – e² + 1 = 0 произошла лишь их перестановка.

Это уникальное свойство позволяет им быть единственными взаимодействующими материальными частицами фермионного типа для обоих подпространств. А реакция аннигиляции (и, соответственно, рождения пары) получает свое логическое завершение (см. рис.4).

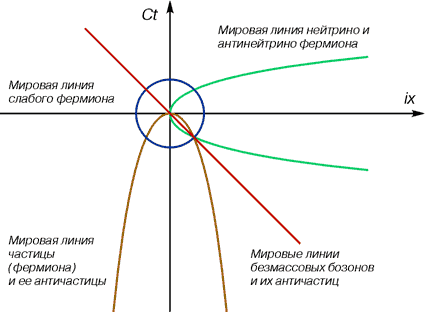
Рис. 4. Реакция аннигиляции. Мировые линии частиц

Получают логическое объяснение все особенности слабых взаимодействий. Как следствие мы можем констатировать, что электрон, позитрон, электронные нейтрино и антинейтрино – суть четыре физические ипостаси одной геометрической сущности. Это же касается и других фермионов.

4.4.7. Поле 2.1.3.1. (Поле Планка)

В отличие от других полей, поле 2.1.3.1 не имеет не скрытых координат, а значит, не наблюдаемо и действует всегда и везде. Так же как и поле слабых фермионов, поле 2.1.3.1 действует в обоих подпространствах. Поле 2.1.3.1 есть закон сохранения в его наиболее общем виде. Поскольку поле определяет кривизну пространства в зависимости от его энергетического состояния, в характеристическое уравнение 2.1.3.1 должна входить постоянная Планка. Группа вращения поля 2.1.3.1 – SU(1, 1). В наблюдаемом подпространстве группа проявит себя как группа U(1), но каждому из множества значений одной переменной будут соответствовать два, противоположных по знаку значения другой переменной.

5. Лирика

Итак, попытаемся разобраться, что же у нас получилось. Наличие ненаблюдаемых координат приводит к существенному ограничению восприятия окружающего нас физического пространства. Наблюдению доступна только четырехмерная оболочка комплексного тора. Поэтому любое сечение (2.1.3.1...2.1.3.7) должно наблюдаться не в виде n-мерного цилиндра, а сферическим в максимуме телом. Другими словами, любое наблюдаемое нами тела (в том числе и мы с Вами) есть «плоскатики» на поверхности тора и о наличии каких-то других его измерений мы можем судить только по особым дополнительным характеристикам взаимодействия между телами и их собственного внутреннего состояния. Кроме того, любая система координат, связанная с любым материальным телом будет системой координат на поверхности тора и, следовательно, будет только относительной.

Геометрически движением комплексного тора является вращение с постоянной угловой скоростью. Это приводит к тому, что на поверхностях равной кривизны все тела имеют одну скорость – скорость света. Нет в природе других действительных скоростей. Поэтому следующим следствием ограниченности нашего восприятия является относительность наблюдаемой скорости. Наблюдаемая составляющая скорости будет зависеть от угла наклона мировых линий частиц в полном соответствии с преобразованиями Лоренца.

Как выше уже констатировалось, физическое пространство не может быть пустым. Любое достаточно обширное пустое пространство будет обладать энергией антигравитации для рождения частиц. От его центра будет направлен вектор движения космических лучей. И этот процесс будет идти до тех пор, пока гравитация материи не уравновесит антигравитацию вакуума и вероятность рождения новых частиц не станет достаточно малой. Таким образом, гравитация ограничивает не только минимальные, но и максимальные размеры физических тел. Ни один физический объект, в том числе область пустого пространства, не может быть больше радиуса кривизны Вселенной. В результате распределение вещества в пространстве будет носить ярко выраженную ячеистую структуру с огромными пустотами и сосредоточением материи на границах этих пустот и сильной дифференциацией по плотности и соответствующей разнознаковой локальной кривизной пространства. Средняя плотность вещества при интегрировании по достаточно большому объему (на Мега-уровне) для любой точки Вселенной будет константой и примерно равна критической, силы тяготения и антигравитации будут в среднем уравновешены, а геометрия наблюдаемого пространства близка к евклидовой (но гиперболические эффекты никто не отменяет). Мировые линии частиц уже не будут аналогами прямых. Средняя уравновешенность сил определит неизменность в среднем расстояний между массами, а мировые линии частиц совпадут с эквидистантами. (см. рис.5).

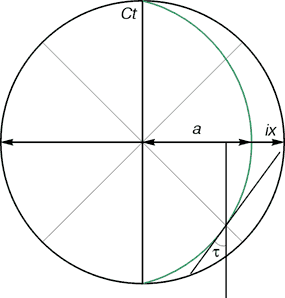
Рис. 5. Мировые линии тел отсчета и пробного в физическом пространстве Вселенной, заполненном веществом с критической плотностью.