Реферат: Геометрия физического пространства
1. Аксиомы
1.1. Физическое пространство Вселенной вещественно.
1.2. Физическое пространство Вселенной не имеет выделенных подпространств.
1.3. Физические и геометрические свойства пространства Вселенной однозначно взаимообусловлены.
2. Основная теорема физического пространства
Физическое пространство Вселенной есть комплексное пространство вида:
![]()
2.1. Идея доказательства:
2.1.1. Физическое пространство Вселенной есть пространство гладких кривых – следствие аксиомы 1.2.
2.1.2. Из всех пространств гладких кривых физическому пространству Вселенной соответствуют пространства кривых четного порядка, описываемых уравнениями с действительными корнями – следствие аксиомы 1.1.
2.1.3. Число характеристических уравнений пространства кривых четного порядка с действительными решениями и отсутствием выделенных (особых) подпространств (в первом приближении – кривыми второго порядка) конечно:
2.1.3.1. (X1)2 – (X2)2 = 0.
2.1.3.2. (X1)2 – (X2)2 + (X3)2 = 0.
2.1.3.3. (X1)2 – (X2)2 – (X3)2 + (X4)2 = 0.
2.1.3.4. (X1)2 – (X2)2 + (X3)2 + (X4)2 = 0.
2.1.3.5. (X1)2 – (X2)2 – (X3)2 + (X4)2 + (X5)2 = 0.
2.1.3.6. (X1)2 – (X2)2 + (X3)2 + (X4)2 + (X5)2 = 0.
2.1.3.7. (X1)2 – (X2)2 – (X3)2 + (X4)2 + (X5)2 + (X6)2 = 0.
2.1.4. Умножение уравнений 2.1.3.1...2.1.3.7 на (–1) даст систему характеристических уравнений сопряженного подпространства.
3. Следствия
3.1. Физическое пространство Вселенной есть двойственно сопряженные овальные гиперповерхности четного порядка 6-мерного проективного пространства над полем комплексных чисел.
3.2. Физические подпространства (сечения, поля, частицы) с размерностью менее 6 есть k-кратные цилиндры над овальной (6–k)-мерной гиперповерхностью.
3.3. Сингулярный базис физического пространства:
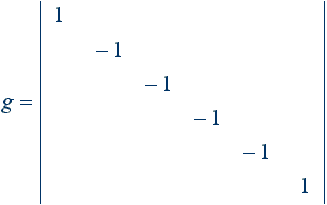
3.3.1. Сингулярный базис сопряженного физического пространства:
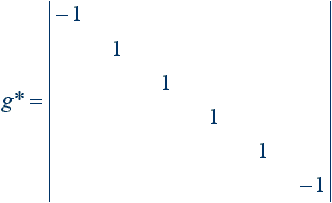
3.4. Группы вращения физического пространства – SU(p, q).
3.5. Мировые линии физических тел – кривые четного порядка с действительными решениями.
4. Подпространства
--> ЧИТАТЬ ПОЛНОСТЬЮ <--