Реферат: Графики и их функции

Теперь рассмотрим функцию y = xr, где r - положительное или отрицательное дробное число. Рассмотрим в качестве примера функцию y = x2,5. Область ее определения - луч. Построим на этом луче графики функций у = х2 (ветвь параболы) и у = х3 (ветвь кубической параболы) - эти графики изображены. Стоит заметить, что на интервале (0;

1) кубическая парабола располагается ниже, а на открытом луче (1; +∞) выше параболы. Нетрудно убедиться в том, что график функции у = х2,5 проходит через точки (0; 0) и (1;

1), как и графики функций у = х2, у = х3. При остальных значениях аргумента х график функции у = х2,5 находится между графиками функций у = х2 и у = х3 (см. приложение 7).

Почему так происходит? Посмотрим:

1). Если 0 < х < 1, то 2). Если х > 1, то

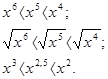
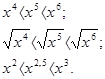
Примерно так же обстоит дело для любой степенной функции вида у = хr, где -неправильная дробь(числитель больше знаменателя). Ее графиком является кривая (см. приложение 8), похожая на ветвь параболы. Чем больше показатель r, тем “круче” устремлена эта кривая вверх.

Свойства функции

D(f) = ;

не является ни четной, ни нечетной;

возрастает на ;

не ограничена сверху, ограничена снизу;

не имеет наибольшего значения; у наим. = 0;

непрерывна;

E(f) = ;

выпукла вниз.

Рассмотрим степенную функцию для случая, когда - правильная дробь . Все рассмотренное в этой главе в отношении функции , или, что то же самое, имеет и отношению к любой степенной функции вида у = хr, где - правильная дробь. График этой функции изображен (см. приложение 9)

Свойства функции, где :

D(f) =;

не является ни четной, ни нечетной;

возрастает на ;

не ограничена сверху, ограничена снизу;

не имеет наибольшего значения; у наим. = 0;

непрерывна;

E(f) = ;

выпукла вверх.

Нам осталось рассмотреть степенную функцию вида . Область ее определения - открытый луч. Выше мы построили график степенной функции y = x - n, где n - натуральное число. При график функции y = x - n похож на ветвь гиперболы. Точно так же дело обстоит для любой степенной функции вида график, которой изображен. Отметим, что график данной функции имеет горизонтальную асимптоту y = 0 и вертикальную асимптоту x = 0.

Свойства функции :

D(f) =;