, (36)

порядка . Радиус сходимости ряда обозначим .

Метод рядов Тейлора решения задачи Коши (23), (24) заключается в построении таблицы приближенных значений по формулам:

,

,, (37)

где - натуральные, , ,, а удовлетворяют неравенствам .

Для программной реализации метода рядов Тейлора необходимы алгоритмы нахождения коэффициентов Тейлора и автоматического выбора величины шага интегрирования.

Нахождение коэффициентов Тейлора

Рассмотрим квадратичную задачу Коши

, (38)

, (39)

где - вещественные или комплексные постоянные, а - вещественная или комплексная переменная.

Подставляя в (38) разложение Тейлора

, (40)

получаем:

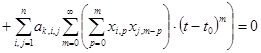(41)

Приводя подобные члены и приравнивая все коэффициенты полученного степенного ряда нулю, получаем искомые формулы:

;

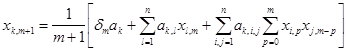, , , (42)

где , .

Аналогичные формулы легко вывести и для общего случая полиномиальной системы степени .

Оценка погрешности и выбор шага

Рассмотрим полиномиальную задачу Коши:

, (43)

, (44)

где , , , а максимальная степень полиномов (степень системы (43)) равна .

Введем обозначения:

, , (45)

и будем предполагать, что .

Теорема.