Реферат: Идентификация параметров осциллирующих процессов в живой природе моделируемых дифференциальными

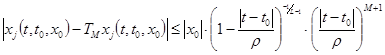, (46)

где

, , (47)

Используя эту теорему несложно построить алгоритм автоматического выбора шага в методе рядов Тейлора по заданной пользователем границе абсолютной (или относительной) погрешности.

1.4.3 Метод Рунге-Кутта

Этим методам посвящено много работ, и они хорошо изложены в много-численных учебниках (см., например, [2,3]).

2. Модели осциллирующих процессов в живой природе

2.1 Модель Лотки

2.1.1 Осциллирующие химические реакции

В некоторых химических реакциях концентрации реагентов осциллируют в следующем смысле. Соединение каких-то начальных веществ приводит к их химическому взаимодействию, в результате чего образуются новые вещества, которые также начинают взаимодействовать с другими реагента-ми. В течении всех этих реакций концентрации реагентов колеблются и, на-конец, все химические преобразования завершаются и в качестве результата остаются какие-то определенные вещества, которые уже не реагируют между собой. Первая математическая модель осциллирующих химических реакций была предложена в работе Лотки [7].

Рассматривается математическая модель взаимодействия на молекулярном уровне веществ на основе следующих предположений:

1. При взаимодействии с молекулой вещества молекула вещества превращается в молекулу вещества . Это описывают в форме молекулярной ре-акции:

(1)

Такую реакцию относят к классу автокаталитических, так как наличие вещества обеспечивает превращение другого вещества в .

2. При взаимодействии с молекулой вещества молекула вещества пре-вращается в молекулу вещества , то есть происходит автокаталитическая молекулярная реакция:

(2)

3. Вещество в то же время необратимо распадается, превращаясь в вещество , то есть происходит молекулярная реакция

(3)

4. Скорости протекания реакций (1), (2), (3) пропорциональны концентрациям веществ в левых частях этих реакций, то есть равны соответственно:

, , , (4)

где символами , , обозначены концентрации веществ , , со-ответственно, а коэффициенты - положительные числа.

5. Скорость изменения концентрации каждого вещества равна сумме скоростей изменения концентраций этого вещества во всех реакциях, в которых оно участвует.

Из условий 1-5 следуют равенства:

,

,

,