Реферат: Інтегральні перетворення Лапласа

В багатьох задачах математичного аналізу розглядаються випадки, в яких кожна точка одного простору ставиться у відповідність деякій точці іншого (або того ж самого) простору. Відповідність між двома точками встановлюється за допомогою перетворення або оператора. В задачу теорії операторів входить докладний опис і класифікація різноманітних видів перетворень і їх властивостей, а також розробка символічних методів, що дозволяють мінімалізувати і спростити обчислення. Застосування операційного метода можна порівняти з логарифмуванням, коли 1) від чисел переходять до логарифмів, 2) над логарифмами проводять дії, що відповідають діям над числами, при тому множенню чисел відповідає більш проста операція складання логарифмів і т.д. 3) від найденого логарифма знов повертаються до числа. В операційному методі широко використовується перетворення Лапласа, яке перетворює певний клас функцій-оригіналів f ( t ) дійсної змінної t в функцію-зображення F ( p ) комплексної змінної p .

1 . Означення перетворення Лапласа . Оригінал і зображення .

Нехай f [ t] -інтегрована на (0,Т) при довільному Т>0 функція, що дорівнює нулю при t>0 : f[t]=0 при t<0. Якщо ця функція при t>0 задовольняє оцінці:

(1.1)

то можна розглянути інтеграл

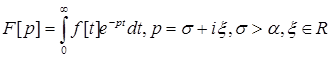(1.2)

Дійсно справджується оцінка

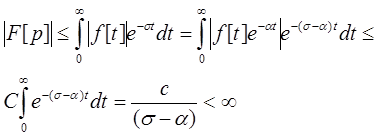(1.3)

При виведенні (1.3) булазастосованаоцінка (1.1). З оцінки (1.3), зокрема,випливає, що . Функція є аналітичною функцією комплексної змінної в півплощині . Для того щоб це перевірити, знаходимо поки формально:

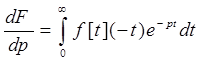(1.4)

Як і при виведенні (1.3), знаходимо

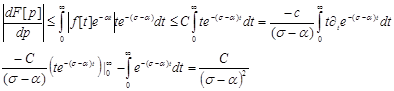(1.5)

Останнє означає що інтеграл рівномірно по Rep>aзбігається і випливає що похідна існує при , і формула (1.4) справедлива при .

Інтеграл (1.2) називається перетворенням Лапласа функції і позначається -. В цьому випадку функція називається оригіналом, а функція –зображенням.

Перетворення Лапласа можна зв’язати з перетворенням Фур’є. Дійсно з (1.2) маємо:

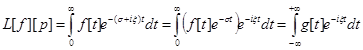
Де (Перетворення Фур’є із знаком «-»)

2. Властивості перетворення Лапласа L

Лінійність.

Доведення:

В силу властивостей інтеграла:

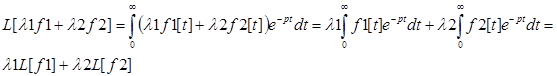
Диференціювання зображення

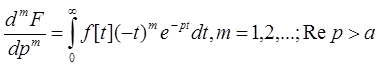
Для m=1 властивість вже встановлено. Для довільногоmвластивість доводиться аналогічно.

Перетворення Лапласа похідних.

Для m=1 за допомогою інтегрування частинами знаходимо

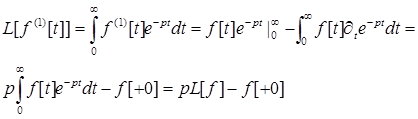
--> ЧИТАТЬ ПОЛНОСТЬЮ <--