Реферат: Інтегральні перетворення Лапласа

При и . Для довільногоmвластивість 2.3 встановлюється за індукцією

Зсув перетворення Лапласа.

Доведення властивості 2.4 очевидно.

Перетворення Лапласа і його подібності.

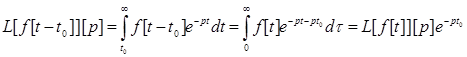
Зсув оригінала в перетворенні Лапласа.

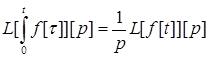
Доведення. Позначимо

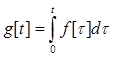
Очевидно, щоg’[t]=f[t], g[+0]=0

Тому за допомогою інтегрування частинами знаходимо

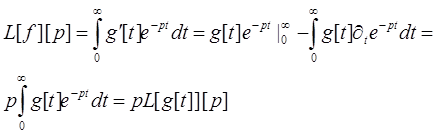
При цьому ми врахували щоg[+0]=0 в силу умови (1.1)

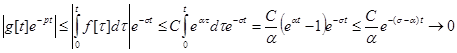
при , , .

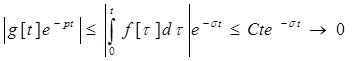
при , , .

Звідси знаходимо

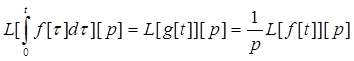
Перетворення Лапласа дробуf[t]/t.

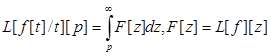
Доведення. ПозначивФ[ p ]=£[ f [ t ]\ t ][ p ] . Знайдемо

Останню рівність про інтегруємо по довільному шляху від р до довільної точки z = Rez =∞

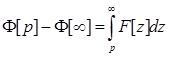
Враховуючи, що в силу (1.3) Ф[∞ ]=0. І отримаємо потрібну властивість (2.8).