Реферат: Інтегральні перетворення Лапласа

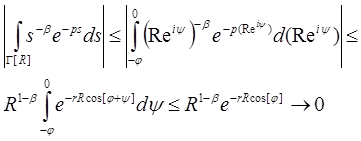
при R→∞.

Перейдемо до границі при R→∞, →0 в рівності (5.3), отримуємо

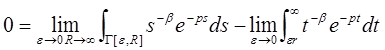
Звідси і із 5.2 встановлюємо (5.1).

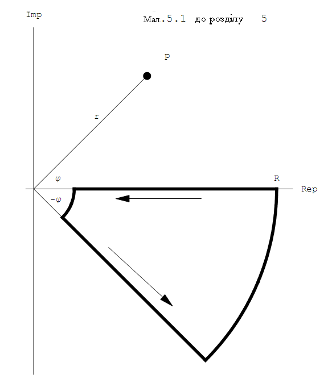
5. Приклади розв’язання базових задач

Зауваження. Функцією-оригіналом називається будь-яка комплексно значна функція f ( t ) дійсного аргументу t , що задовольняє умовам:

1°.f ( t ) інтегрована на будь-якому скінченому інтервалівісі t (локально інтегрована).

2°.Для усіх від’ємних t

3°. f ( t ) зростає не швидше ніж показникові функція, тобто існують такі сталі і , що для усіх t

Задача1. Показати що функція є функцією-оригіналом.

Розв’язання

Дійсно, функція f ( t ) локально інтегрована

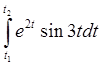
існує для будь-яких скінчених і . Умова 2° виконана в силу завдання функції.

І врешті решт, для будь-яких дійсних

,

Тобто в якості М в умові 3° можна вибрати довільне число >1

Задача2. Користуючись означенням, знайти означення функції

Розв’язання

Для функції маємо . Тому зображення буде в усякому разі визначене і аналітичне на півплощині . Маємо:

Тобто, . Ця функція аналітична при , і крім того вона аналітична всюди, за виключенням точки . Це не суперечить означенню, так як останнє гарантує аналітичність при , але не стверджує, що якщо , тоді функція буде всюди аналітична.

Задача3. Знайти зображення функції

Розв’язання