Реферат: Інтегральні перетворення Лапласа

Доведемо, що f[t]=0, при t<0. Для цього розглянемо інтеграл по замкненому контуру в півплощині , що складається з дуги кола радіуса R і відрізка прямої (мал. 4.2). За теоремою Коши :

В силу леми Жордана інтеграл по дузі кола прямує до нуля при t<0 і R→∞. Інтеграл що залишився в границі переходить до інтегралу по прямій , дорівнює нулю при t<0. Покажемо нарешті що перетворення Лапласа в точці p = q ( ) співпадає з F [ q ]. За допомогою формули Коши знаходимо при

■

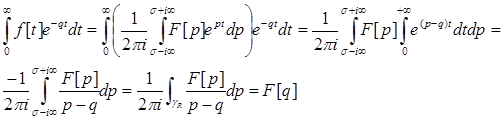Прививеденні ми врахували що інтеграл по прямій можна замінити на інтеграл за замкненим контуром , так як

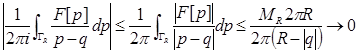при R→∞

Лема Жордана. Нехай t>0 і - півколо радіуса R в півплощині . Якщо функція задовольняє умовам:

функція неперервна при , ,

Тоді при R→∞

Доведення

Зробимо заміну змінної інтегрування

z=R.

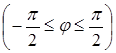Тоді справедлива оцінка інтеграла

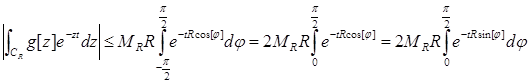
Як відомо, при . Продовжимо оцінку інтеграла

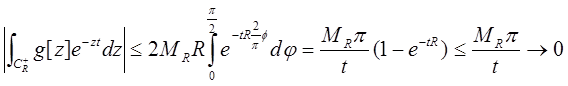
При R→∞. Лему доведено■

Задача Знайти перетворення Лапласа функції

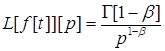(5.1)

Введена гамма-функція

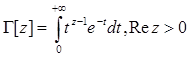
Розглянемо спочатку L[f[t]][p] при p>0. За допомогою простої заміни змінних знаходимо

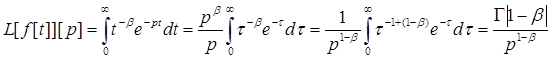
Нехай далі і. Для визначеності будемо вважати , (випадок розглядається аналогічно). Покладемо . Легко перевіряється що ps=t – додатне число.

Далі маємо:

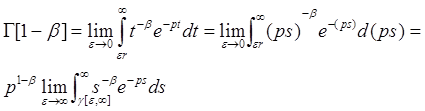(5.2)

де - відрізок променя . Побудуємо замкнений контур (мал. 5.1). За теоремою Коши: