Реферат: Интегралы Дифференциальные уравнения

На основе ряда распределения можно определить среднее значение случайной дискретной величины как меру, которая объединяет значения случайной дискретной величины и их вероятности. Среднее значение есть взвешенная средняя всех возможных значений случайной величины, роль весов (частот) играют вероятности.

Ожидаемое среднее значение случайной величины называется математическим ожиданием М(Х) (оценкой, которую ожидают получить).

Математическое ожидание случайной дискретной величины X (т.е. принимающей только конечное или счетное множество значений x1, x2,…, хп соответственно с вероятностями р1, p2,…, рп) равно сумме произведений значений случайной величины на соответствующие им вероятности:

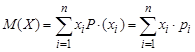. (1)

Свойства математического ожидания случайной дискретной величины

Математическое ожидание случайной дискретной величины обладает следующими свойствами:

1. M(C) = С,

где С – постоянная величина.

2. М (С·Х) = С·М(Х),

где С – постоянная величина.

3. М (Х1 ± Х2 ±…± Хn) = М(Х1) ± М(Х2) ±…± М(Хn). (2)

4. Для конечного числа пнезависимых случайных величин:

М (Х1∙ Х2∙…∙Хn)= М(Х1) ∙М(Х2) ∙…∙М(Хn). (3)

5. М (Х–C) = М(Х) – C.

Следствие. Математическое ожидание отклонения значений случайной величины X от ее математического ожидания равно нулю:

М [Х – М(Х)] = 0. (4)

6. Математическое ожидание среднего арифметического значения п одинаково распределенных взаимно независимых случайных величин равно математическому ожиданию каждой из величин:

. (5)

Случайные дискретные величины называются одинаково распределенными, если у них одинаковые ряды распределения, а следовательно, и одинаковые числовые характеристики.

Пусть Х1, Х2,…, Хn – одинаково распределенные случайные величины, математические ожидания каждой из которых одинаковы и равны а. Тогда математическое ожидание их суммы равно nаи математическое ожидание средней арифметической равно а:

.

Ожидаемое среднее значение функции случайной величиныожидаемое среднее значение можно вычислять как функцию случайной величины. Пусть h(X) – функция случайной величины X. Ожидаемое значение функции дискретной случайной величины:

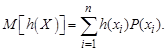(6)

Функция h(X) может быть любой, например X 2,3Х 4, logX. Разберем простой пример, когда h(X) – линейная функция от X, т.е. h(X)= аХ+ b, где а, b – числовые параметры.

Ожидаемый ежемесячный доход от продаж продукции составляет 5400 условных денежных единиц. Для линейной функции случайной величины вычисления M[(h(x)] можно упростить, так как из свойств математического ожидания следует, что

M (аХ+ b) = аM(Х) + b,

где a, b – числовые параметры.

Формула (5) подходит для любых случайных величин как дискретных, так и непрерывных.

Дисперсия дискретной случайной величины