Реферат: Интегралы Дифференциальные уравнения

,

где – число всех исходов эксперимента, -число благоприятствующих событию исходов. Это так называемая классическая схема.

Пусть некоторый эксперимент повторяется раз.

Схема Бернулли имеет место при соблюдении трех условий.

1. Каждое повторение имеет два исхода.

2. Повторения независимы.

3. Вероятность появления события постоянна и не меняется при повторениях.

Тогда вероятность появления события раз при испытаниях можно найти по формуле

,

где – число сочетаний из элементов по, .

Если события такие, что

1. попарно не пересекаются, то есть .при

2. ,

то говорят что они образуют полную группу событий.

Теорема (формула полной вероятности). Если – полная группа событий и , то

.

Теорема (формула Байеса) Если – полная группа событий и , то

,

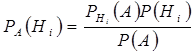Случайной величиной называют любую числовую функцию заданную на множестве . Случайные величины делятся на дискретные и непрерывные.

Дискретной случайной величиной называется случайная величина принимающая не более чем счетное число значений. Дискретную случайную величину удобно задавать в виде таблицы

где – вероятность того, что случайная величина примет значение при.

Математическим ожиданием дискретной случайной величины называется число = .

Свойства математического ожидания

1.

2.

3. .

Дисперсией дискретной случайной величины называется число

Свойства дисперсии