Реферат: Интерактивные графические системы
1. Устанавливаем kd =1
( k - номер обрабатываемой поверхности в примитиве d)
Устанавливаем FLAG=0
(индикатор отсутствия (0) или наличия (1) решений)
2. Решается система (*)
3. Если решений нет, то увеличиваем kd на 1 (до тех пор, пока kd £ Kd ) и возврат на шаг 2.
4. Если решения есть (в общем случае ![]() решений), то устанавливаем
решений), то устанавливаем ![]() (где
(где ![]() - номер текущего решения поверхности под номером kd )
- номер текущего решения поверхности под номером kd )
5. Для всех Kd поверхностей, кроме kd проверяют условие : ![]() (где r - текущий номер поверхности в d-ом примитиве)
(где r - текущий номер поверхности в d-ом примитиве)
6. Если условие не выполняется, то увеличиваем ![]() на 1 (пока
на 1 (пока ![]() ) и возврат на шаг 5.
) и возврат на шаг 5.
7. Если условие 5 выполнено и FLAG=0, то точка ![]() размещается в две первые строки матрицы d, а в две первые строки матрицы WHO заносится номер kd .
размещается в две первые строки матрицы d, а в две первые строки матрицы WHO заносится номер kd .
8. Если условие 5 выполнено и FLAG=1, то
(**) точка ![]() ближе к точке (XF , YF , ZF ), чем точка, находящаяся в первой строке матрицы T.
ближе к точке (XF , YF , ZF ), чем точка, находящаяся в первой строке матрицы T.
(***) точка ![]() дальше от точки (XF , YF , ZF ), чем точка, находящаяся во второй строке матрицы T.
дальше от точки (XF , YF , ZF ), чем точка, находящаяся во второй строке матрицы T.
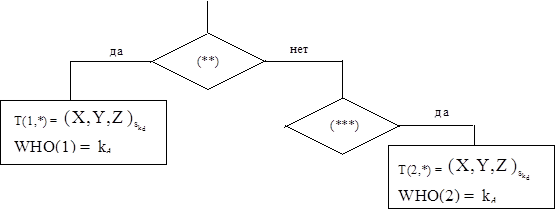
9. FLAG=1, увеличиваем kd на 1 (пока kd £ Kd ) и возврат на шаг 2.
Пересечение луча с комбинацией примитива.
Когда задача определения точек пересечения луча с примитивами решена, в полученной совокупности необходимо выделить точку, ближайшую к наблюдателю, т. е. видимую. Для этого все матрицы WHO и матрица Т для каждого из примитивов сводятся в единые блочные матрицы WHO и Т.
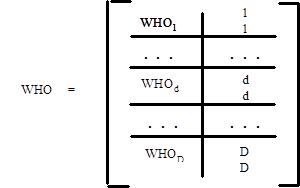
Матрица Т переформируется таким образом, чтобы в её первой строке помещалась точка, ближайшая к источнику луча, порядок остальных точек может быть произвольным. Синхронно сортируется матрица WHO для того, чтобы не терялась связь между точкой и конкретной поверхностью. Когда таким образом выделена ближайшая точка (XБ , YБ , ZБ ) следует проверить её принадлежность к поверхности объекта. Для этого оценивается положение точки относительно каждого из примитива объекта. Положение точки и каждого примитива определяется функцией принадлежности, а относительно положения точки (XБ , YБ , ZБ ) и объекта О = f ( П1 , . . , ПD ), устанавливается путём попарной проверки функции принадлежности j (XБ , YБ , ZБ , ПD ) и функции d = 1(1)D ( d = 1. . D
Пример:
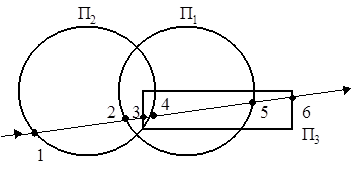
O = ( П1 ï П2 ) ï П3
Световой луч пересекает объект в точках с 1 по 6, ближайшей к источнику луча является точка 1. Функция принадлежности этой точки:
j ( X1 , Y1 , Z1 , П1 ) = -1
j ( X1 , Y1 , Z1 , П2 ) = 0
j ( X1 , Y1 , Z1 , П3 ) = -1
j ( X1 , Y1 , Z1 , П1 ï П2 ) = -1
j ( X1 , Y1 , Z1 , ( П1 ï П2 ) ï П3 ) = -1
Таким образом точка 1 будучи ближайшей к источнику луча не является видимой, так как находится вне объекта.
Если ближайшая точка не находится на поверхности объекта ( см. пример ), она исключается из дальнейшего рассмотрения. Среди оставшихся точек снова выделяются ближайшие и процесс продолжается до тех пор, пока либо не исключатся все точки, либо не будет найдена точка, одновременно и ближайшая, и принадлежащая объекту, так как матрицы WHO и Т перестраивались синхронно, то номера поверхности и примитива для видимой точки прочитываются из первой строки матрицы WHO.
Если объект и прямая заданы в объектной системе координат, то наиболее общий критерий к ближайшей точке
( ХF - ХБ )2 + ( YF - YБ )2 + ( ZF - ZБ )2 <= ( ХF -Xn )2 + (YF - Yn )2 + ( ZF - Zn )2
для любого n.
В частных случаях критерий может быть упрощен:
(XБ , YБ , ZБ ) : abs (ХF - ХБ ) <= abs ( ХF -Xn ) для " n
(XБ , YБ , ZБ ) : abs (YF - YБ ) <= abs (YF - Yn ) для " n
(XБ , YБ , ZБ ) : abs ( ZF - ZБ ) <= abs ( ZF - Zn ) для " n
Применение упрощенных критериев оправдано в том случае, когда априорно известно не параллельность любого светового луча плоскостям Yz, Xz и XY.
Например: последний критерий может быть использован при моделировании аэрофотосъёмки.
Определение затенённых точек.
Точки объекта видимые рецепторами подразделяются на два класса:
- точки, освещённые прямым светом;