Реферат: Исследование функций

Пример 1. у = х³ , у' = 3х² , у'(0) = 0, но

в точке х₀ = 0 нет экстремума.

Точками, подозрительными на экстремум функции f(x) на интервале (a, b), являются точки, в которых производная существует и равна 0 либо она не существует или равна бесконечности. На рисунках функции имеют минимум в точке х₀ = 0:

f'(0) = 0 f'(0) $f'(0) = ¥

Рассмотрим достаточные условия существования в точке локального экстремума, которые позволят ответить на вопрос: «Есть ли в точке экстремум и какой именно – минимум или максимум?».

Теорема 1 (первое достаточное условие экстремума). Пусть непрерывная функция f(x) дифференцируема в некоторой проколотой окрестности U(x₀ ) точки х₀ (проколотая окрестность означает, что сама точка х₀ выбрасывается из окрестности) и непрерывна в точке х₀ . Тогда:

1) если (1)

то в точке х₀ – локальный максимум;

2) если (2)

то в точке х₀ – локальный минимум.

Доказательство.

Из неравенств (1) и следствия 3 теоремы Лагранжа (о монотонности функции) следует, что при х < х₀ функция не убывает, а при х > х₀ функция не возрастает, то есть

(3)

Следовательно, из (3) получаем, что в точке х₀ функция имеет локальный максимум.

Аналогично можно рассмотреть неравенства (2) для локального минимума:

f (x) f (x)

f'(х) ³ 0 f'(х) £ 0 f'(х) £ 0 f'(х) ³ 0

Теорема доказана.

Пример 2. Исследовать на монотонность и локальный экстремум функцию с помощью производной первого порядка.

Решение. Найдем стационарные точки функции:

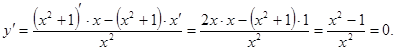
Þ х² –1 = 0 Þ х₁ = –1, х₂ = 1.

Заметим, что данная функция не определена в точке х = 0. Следовательно:

х	(–¥; –1)	–1	(–1; 0)	0	(0; 1)	1	(1; +¥)
у'	+	0	–	–	–	0	+
у		–2		–		2

max min

То есть функция возрастает на интервалах (–¥; –1) и (1; +¥), убывает на интервалах (–1; 0), (0; 1), имеет локальный максимум в точке

х₁ = –1, равный у_max (–1) = –2; имеет локальный минимум в точке х₂ = 1,

у_min (1) = 2.