Реферат: Исследование функций

3. (см. пример 2). Исследуем функцию на монотонность и экстремум:

х	(–¥; –1)	–1	(–1; 0)	0	(0; 1)	1	(1; +¥)
у'	+	0	–	–	–	0	+
у		–2		–		2

max min

4. (см. пример 5). Исследуем функцию на выпуклость и найдем точки перегиба.

х	(–¥; 0)	0	(0; +¥)
у''	–	–	+
у	выпукла вверх	–	выпукла вниз
функция не определена

Несмотря на то, что функция поменяла характер выпуклости при переходе через точку х = 0, но в ней нет перегиба, так как в этой точке функция не определена.

5. (см. примеры 6 и 7). Найдем асимптоты функции:

а) х = 0 – вертикальная асимптота;

б) у = х – наклонная асимптота.

6. Точек пересечения с осями координат у данной функции нет, так как 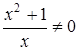, при любых х Îú, а х = 0 ÏD(у).

7. По полученным данным строим график функции:

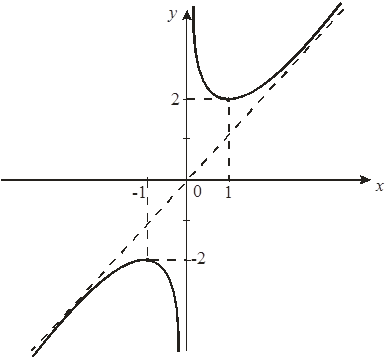
Пример 10. Построить график функции .

Решение.

1. D(у) = (–¥; –1) È (–1; 1) È (1; +¥).

2. 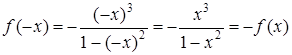– функция нечетная. Следовательно, график функции будет симметричен относительно начала координат.

3. Исследуем функцию на монотонность и экстремум:

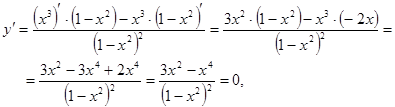
3х² – х⁴ = 0, х² · (3 – х² ) = 0, х₁ = 0, х₂ = , х₃ = .

х	(–¥;)		(; 0)	–1	(–1; 0)	0	(0; 1)	1	(1; )		(; +¥)
у'	–	0	+	–	+	0	+	–	+	0	–
у		2,6		–		0		–		–2,6

4. Исследуем функцию на выпуклость и точки перегиба:

х = 0 – точка, подозрительная на перегиб.

х	(–¥; –1)	–1	(–1; 0)	0	(0; 1)	1	(0; +¥)
у''	+	–	–	0	+	–	–
у	выпукла вниз	–	выпукла вверх	0	выпукла вниз	–	выпукла вниз
перегиб

5. Найдем асимптоты функции:

а) х = –1, х = 1 – вертикальные асимптоты.