Реферат: Исследование функций

Доказательство.

Если бы f'' (х₀ ) < 0 или f'' (х₀ ) > 0, то по теореме 3 в точке х₀ функция f(х) была бы выпукла вверх или вниз. Следовательно, f''(х₀ ) = 0.

Теорема доказана.

Теорема 5 (достаточное условие перегиба). Если функция f(х) дважды непрерывно дифференцируема в окрестности точки х₀ и при переходе через точку х₀ производная f''(х) меняет знак, то точка х₀ является точкой перегиба функции f(х).

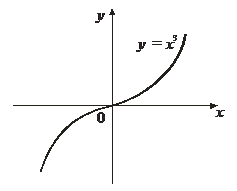
Пример 4. Исследовать на выпуклость и найти точки перегиба функции у = х³ .

Решение. у' = 3х² , у'' = 6х = 0 Þ х₀ = 0 – точка, подозрительная на перегиб.

В точке х₀ = 0 функция у = х³ имеет перегиб:

х	(–¥; 0)	0	(0; +¥)
у''	–	0	+
у	выпукла вверх	0	выпукла вниз
точка перегиба

Пример 5. Исследовать на выпуклость и найти точки перегиба функции .

Решение. В примере 3 мы уже находили вторую производную данной функции . Так как то точек подозрительных на перегиб нет. Рассмотрим промежутки выпуклости:

х	(–¥; 0)	0	(0; +¥)
у''	–	–	+
у	выпукла вверх	–	выпукла вниз
функция не определена

2. 3 Асимптоты графика функции

Асимптотой будем называть прямую, к которой график функции неограниченно близко приближается. Различают вертикальные и наклонные асимптоты.

Прямая х = х₀ называется вертикальной асимптотой графика функции f(х), если хотя бы один из пределов f(х₀ – 0) или f(х₀ + 0) равен бесконечности.

Пример 6. Найти вертикальные асимптоты функций:

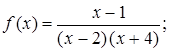а) б) в)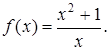

Решение. Вертикальными асимптотами функций будут прямые х = х₀ , где х₀ – точки, в которых функция не определена.

а) х = 3 – вертикальная асимптота функции . Действительно, ;

б) х = 2, х = –4 – вертикальные асимптоты функции 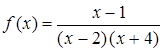. Действительно,

,

;

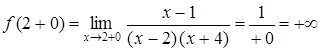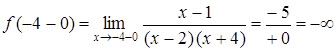в) х = 0 – вертикальная асимптота функции 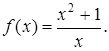Действительно, .

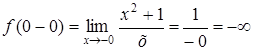Прямая у = kx + b называется наклонной асимптотой графика непрерывной функции f(х) при х ® +¥ или х ® –¥, если f(х) = kx + b + α(х), , то есть если наклонная асимптота для графика функции f(х) существует, то разность ординат функции f(х) и прямой у = kx + b в точке х стремится к 0 при х ® +¥ или при х ® –¥.

Теорема 6. Для того чтобы прямая у = kx + b являлась наклонной асимптотой графика функции f(х) при х ® +¥ или х ® –¥, необходимо и достаточно существование конечных пределов:

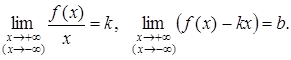(4)

Следовательно, если хотя бы один из данных пределов не существует или равен бесконечности, то функция не имеет наклонных асимптот.

Пример 7. Найти наклонные асимптоты функции

Решение. Найдем пределы (4):

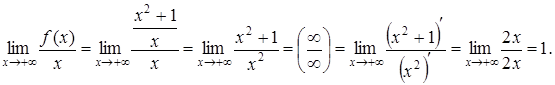
Следовательно, k = 1.