Реферат: Исследование функций

(f'(х₀ ) = 0), в которой f''(х₀ ) > 0, то в точке х₀ функция имеет локальный минимум. Если же f''(х₀ ) < 0, то в точке х₀ функция имеет локальный максимум.

Доказательство. Пусть для определенности f''(х₀ ) > 0. Тогда

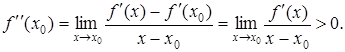
Следовательно:

при х< х₀ , f'(х) < 0,

при х> х₀ , f'(х) > 0.

Поэтому по теореме 1 в точке х₀ функция имеет локальный минимум.

Теорема доказана.

Пример 3. Исследовать на экстремум функцию с помощью второй производной.

Решение. В примере 2 для данной функции мы нашли первую производную и стационарные точки х₁ = –1, х₂ = 1.

Найдем вторую производную данной функции:

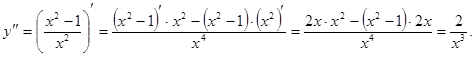
Найдем значения второй производной в стационарных точках.

Þ в точке х₁ = –1 функция имеет локальный максимум;

Þ в точке х₂ = 1 функция имеет локальный минимум (по теореме 2).

Заметим, что теорема 1 более универсальна. Теорема 2 позволяет проанализировать на экстремум лишь точки, в которых первая производная равна нулю, в то время как теорема 1 рассматривает три случая: равенство производной нулю, производная не существует, равна бесконечности в подозрительных на экстремум точках.

2.2 Исследование функций на выпуклость и вогнутость. Точка перегиба

Пусть функция f(х) задана на интервале (a, b) и х₁ , х₂ – любые различные точки этого интервала. Через точки А (х₁ , f(х₁ )) и В (х₂ , f(х₂ )) графика функции f(х) проведем прямую, отрезок АВ которой называется хордой. Уравнение этой прямой запишем в виде у = у(х).

Функция f(х) называется выпуклой вниз на интервале (a, b), если для любых точек х₁ , х₂ Î (a, b), а £ х₁ < х₂ £b, хорда АВ лежит не ниже графика этой функции, т. е. если f(х) £ у (х), œ х Î[х₁ , х₂ ] Ì (a, b):

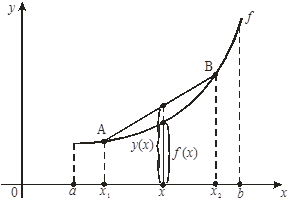
Заметим, что выпуклую вниз функцию иногда называют вогнутой функцией. Аналогично определяется выпуклость функции вверх.

Функция f(х) называется выпуклой вверх на интервале (a, b), если для любых точек х₁ , х₂ Î (a, b), а £ х₁ < х₂ £b, хорда АВ лежит не выше графика этой функции, т. е. если f(х) ³ у (х), œ х Î[х₁ , х₂ ] Ì (a, b):

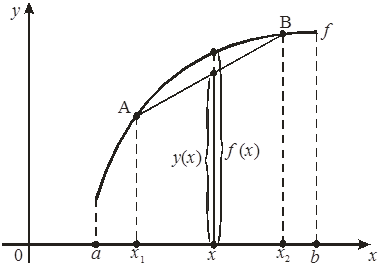
Теорема 3 (достаточное условие выпуклости). Если f(х) – дважды непрерывно дифференцируема на интервале (a, b) и

1) f''(х) > 0, œ х Î(a, b), то на (a, b) функция f(х) выпукла вниз;

2) f''(х) < 0, œ х Î(a, b), то на (a, b) функция f(х) выпукла вверх.

Точка х₀ называется точкой перегиба функцииf(х), если $d – окрест-ность точки х₀ , что для всех х Î (х₀ – d, х₀ ) график функции находится с одной стороны касательной, а для всех х Î (х₀ , х₀ + d) – с другой стороны каса-тельной,проведенной к графику функции f(х) в точке х₀ , то есть точка х₀ – точка перегиба функции f(х), если при переходе через точку х₀ функция f(х) меняет характер выпуклости:

х₀ – d х₀ х₀ + d