Реферат: Исследование функций

Следовательно, b = 0.

Таким образом, функция имеет наклонную асимптоту

у = kx + b = 1 · х + 0 = х.

Ответ: у = х – наклонная асимптота.

Пример 8. Найти асимптоты функции .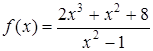

Решение.

а) функция неопределенна в точках х₁ = –1, х₂ = 1. Следовательно, прямые х₁ = –1, х₂ = 1 – вертикальные асимптоты данной функции.

Действительно, .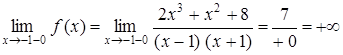

;

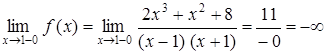б) у = kx + b.

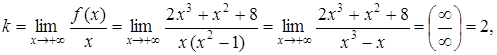
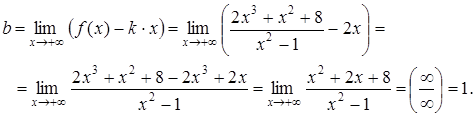
Следовательно, у = 2х + 1 – наклонная асимптота данной функции.

Ответ: х₁ = –1, х₂ = 1 – вертикальные, у = 2х + 1 – наклонная асимп-

тоты.

2.4 Общая схема построения графика функции

1. Находим область определения функции.

2. Исследуем функцию на периодичность, четность или нечетность.

3. Исследуем функцию на монотонность и экстремум.

4. Находим промежутки выпуклости и точки перегиба.

5. Находим асимптоты графика функции.

6. Находим точки пересечения графика функции с осями координат.

7. Строим график.

Прежде чем перейти к примерам, напомним определения четности и нечетности функции.

Функция у = f(х) называется четной , если для любого значения х, взятого из области определения функции, значение (–х) также принад-лежит области определения и выполняется равенство f(х) = f(–х). График четной функции симметричен относительно оси ординат .

Функция у = f(х) называется нечетной для любого значения х, взятого из области определения функции, значение (–х) также принадлежит об-ласти определения, и выполняется равенство f(–х) = –f(х). График не-четной функции симметричен относительно начала координат .

Пример 9. Построить график .

Решение. Мы используем данные, полученные для этой функции в других примерах.

1. D(у) = (–¥; 0) È (0; +¥).