Реферат: Исследование операций
x3 =5 x3 =4
Z=5993 Z=5991
| Вершина | Ограничение | № ограничения |
| 2 | x1 | 7 |
| 3 | x1 | 7 |
| 4 |
x1
x2 |
7 8 |
| 5 |
x1
x2 |
7 8 |
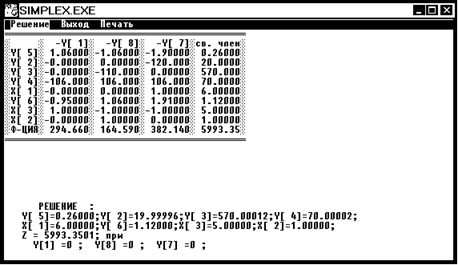
Вывод:
В результате решения я получил, что целочисленное оптимальное решение получается в вершине 4, так как все значения x1 =6, x2 =1,x3 =5 в этой вершине целочисленные и Z5 (5991)<Z4 (5993), следовательно получено оптимальное решение. Висящая вершина 5 и прозондированные 1,2,3,4.
Плановые задания:
![]() , где P – плановое задание тыс. тонн,q – производительность состава,x – количество составов,i – номер предприятия.
, где P – плановое задание тыс. тонн,q – производительность состава,x – количество составов,i – номер предприятия.
Для предприятия 1:
![]() тыс. тонн;
тыс. тонн;
Для предприятия 2:
![]() тыс. тонн;
тыс. тонн;
Для предприятия 3:
![]() тыс. тонн.
тыс. тонн.
Нелинейное программирование.
Задача математического программирования называется нелинейной, если нелинейны ограничения или целевая функция.
Задачи нелинейного программирования бывают выпуклого и невыпуклого программирования, с ограничениями и без ограничений, с квадратичными или сепарабельными целевыми функциями. Задачи нелинейного программирования имеют множество экстремальных точек, и сложность решения заключается в выделении глобального оптимума, а не локального как это делается в большинстве классических методов.
Разделяют задачи безусловной и условной оптимизации. Задачами безусловной оптимизации называются задачи оптимизации функции многих переменных без дополнительных ограничений. Существуют следующие методы безусловной оптимизации: покоординатного спуска, градиентные, сопряженных направлений, метод Ньютона. Задачами условной оптимизации называются задачи о оптимизации целевой функции многих переменных f(x1 , …, xn ) при условии, что эти переменные удовлетворяют следующим ограничениям:
qi (x1 , …, xn ) = 0, ![]()
или
dj (x1 , …, xn ) ![]() 0,
0, ![]()
Решение задачи основывается на линейной или квадратичной аппроксимации целевой функции для определения приращений x1 , …,xn на каждой итерации.