Реферат: Исследование операций
Решение:
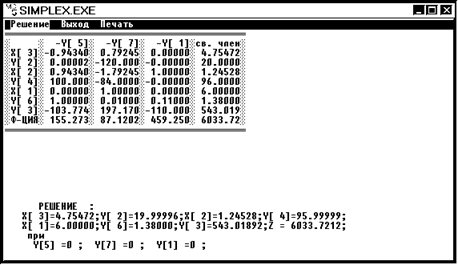
2. Вершина 2 x1 = 6 x2 = 1,2 x3 = 4,8 Z2 = 6033,7212
Мы получили одно целочисленное решение x1 = 6, следовательно дальнейшее ветвление мы будем проводить по x2 или x3 .
Решаем ветвь 2. К ограничениям задачи ЛП добавляем ограничение б.
Седьмым ограничением становится ограничение x1 
7.
Решение:
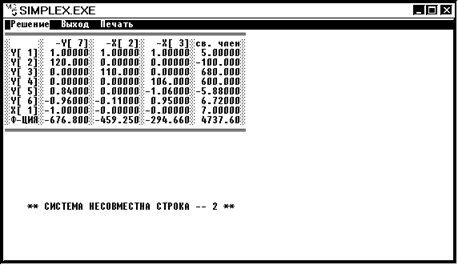
Второй строкой является ограничение задачи ЛП по максимально возможному объему руды с 2 предприятия:
120x1 
740 или x1 6,16666, что противоречит введенному нами условию 6 (б) x1 7. Дальнейшее ветвление из вершины 3 невозможно.
Продолжим ветвление из вершины 2. Как было уже сказано выше, мы можем продолжить ветвление по x2 или x3 . Продолжим ветвление по x2 . x2 = 1,2, следовательно восьмое ограничение для 1 ветви будет x2 1, а для другой x2 
. Движемся сначала по ветви 1 в вершину 4.
Решение:
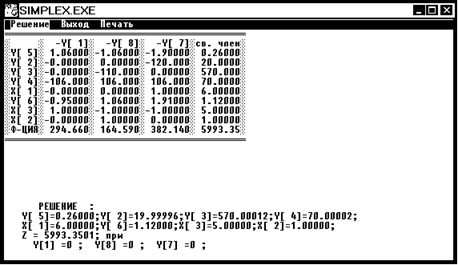
X1 = 6 x2 = 1 x3 = 5 Z4 = 5993,3501
Мы получили, что все три переменных имеют целочисленное значение,
но, чтобы данное решение являлось решением задачи ЦЛП необходимо и достаточно показать, что при ветвлении по ветви 2 в вершине 5 мы получим значение целевой функции Z5 <Z4 . Найдем решение в вершине 5.
Решение:
Z5 = 5991,0396, следовательно Z5 < Z4 , значит в вершине 4 мы получили решение задачи ЦЛП.
Интерпретация решения с помощью блок – схемы:
x1 =6,1
Z1 =6048 x2 =0,9
x3 =4,9
x1 6 x1 7
x1 =6
x2 =1,2 Система
x3 =4,8 несовместна
 |  |
x2 1 x2 2
x1 =6 x1 =5,6