Реферат: Исследование операций

В некоторых задачах целочисленные значения могут быть равны только 0 или 1, тогда такие задачи называются задачами с булевыми переменными.

Задачу целочисленного линейного программирования можно решить как задачу линейного программирования, а затем округлить полученное решение. Однако такой способ допустим только при условии, что значения переменных настолько большие, что погрешностью, вызываемой округлением можно пренебречь. Если же в результате решения переменная принимает малое значение, то ее округление может привести к очень далекому от оптимального решения. Применяются два способа решения задач ЦЛП – метод отсечений и метод ветвей и границ.

Решение задачи ЦЛП методом отсечения :

1. Решение задачи как задачи ЛП.

2. Если мы получили целочисленное решение, то оно и является решением задачи ЦЛП.

3. Если мы получаем нецелочисленное решение, то мы к системе ограничений задачи ЛП прибавляем такое ограничение, что полученное нецелочисленное оптимальное решение не может содержаться во множестве допустимых решений и, таким образом, формируем новую задачу ЛП и решаем ее. Цикл повторяется до тех пор пока не будет получено целочисленное решение (решение задачи ЦЛП (если оно существует)).

Решение задачи ЦЛП методом ветвей и границ :

1. Решаем задачу как задачу ЛП.

2. Если мы получим оптимальные целочисленные решения задачи ЛП, то они являются также и оптимальными решениями задачи ЦЛП.

3. Если мы не получим целочисленных решений, то целевая функция Z₁ задачи ЛП становится верхней границей оптимального значения Z задачи ЦЛП, потому что значение целевой функции Z при введении в дальнейшем новых ограничений для получения оптимальных целочисленных решений уменьшается.

4. Затем производится ветвление по одному из нецелочисленных оптимальных решений задачи ЛП. Ветвление осуществляется с использованием некоторых правил по следующей схеме: если nxn+1, то 1) xn; 2) xn+1, где х – нецелочисленное оптимальное решение задачи ЛП, по которому мы осуществляем ветвление,n – ближайшее целое к х не превышающее х.

Правила ветвления:

1) Выбирается переменная, у которой дробная часть наиболее близка к 0,5.

2) Выбирается переменная с наибольшим приоритетом по какому — либо качественному или количественному значению.

3) Переменная выбирается произвольно.

Ограничения введенные при ветвлении добавляются к ограничениям задачи ЛП.

В каждой из вершин находим оптимальные решения полученных путем добавления новых ограничений задач ЛП – 2 и ЛП – 3. Если не у одной из них мы не получили целочисленных оптимальных решений, то мы выбираем ту вершину, в которой получено наибольшее значение целевой функции и производим дальнейшее ветвление. Так продолжается до получения целочисленного оптимального решения одной из задач ЛП.

Вершина называется прозондированной , если:

1) Мы нашли в ней оптимальное целочисленное решение – решение задачи ЦЛП.

2) В данной вершине нет оптимальных решений задачи ЛП.

3) Значение Z в оптимальном решении задачи ЛП не больше текущей нижней границы.

Прочие вершины называются висящими .

Решение задачи методом целочисленного линейного программирования.

Метод ветвей и границ.

Начальные условия берутся из решения задачи ЛП (решение см. выше).

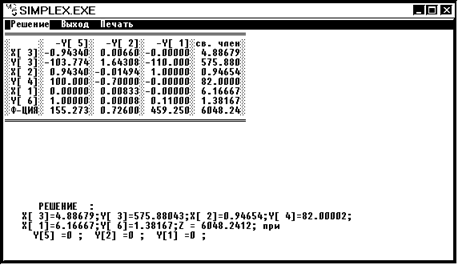
1. Вершина 1 x₁ = 6,17 x₂ = 0,9 x₃ = 4,9 Z₁ = 6048,24

Начнем ветвление по x₁ = 6,17, тогда получаем дополнительные ограничения а) x₁ 6 (1 ветвь) б) x₂ 7 (2 ветвь).

Решаем сначала ветвь 1. К ограничениям задачи ЛП добавляем ограничение а.