Реферат: Исследование операций
-0,84x1 + 1,06x3 
0 – по минимально допустимому содержанию
полезного компонента в руде.
Решение 1.
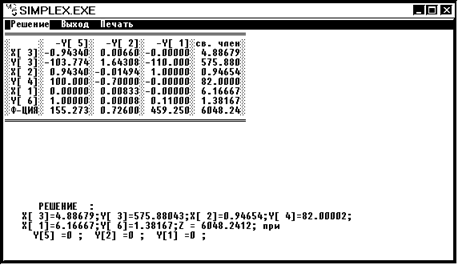
x1 = 6,17 x2 = 0,95 x3 =4,88 Z1 = 6048,24
2. Так как x1 =6,17 – максимально возможный, то коэффициент при x1 в
целевой функции Z2 будет равен 676,8.
Так как x2 =0,95;x2 < 1,87, то коэффициент при x2 в целевой функции Z2 будет равнятся -79,75.
Так как x3 =4,88; 3,96 < 4,88 <5,66, следовательно x3 попадает в интервал 3,96 – 5,66,следовательно коэффициент при x3 в целевой функции Z2 будет равен 40,28.
Следовательно Z2 = 676,8x1 – 79,75x2 + 40,28x3
Решение 2.
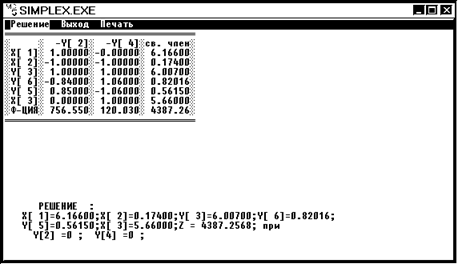
x1 = 6,17 x2 = 0,17 x3 = 5,66 Z2 = 4387,26
3. Так как x1 =6,17 – максимально возможный, то коэффициент при x1 в
целевой функции Z3 будет равен 676,8.
Так как x2 =0,17;x2 < 1,87, то коэффициент при x2 в целевой функции Z3 будет равнятся -79,75.
Так как x3 =5,66 – максимально возможный, то коэффициент при x3 в
целевой функции Z3 будет равен 294,68.
Следовательно Z3 = 676,8x1 – 79,75x2 + 294,68x3
Решение 3.
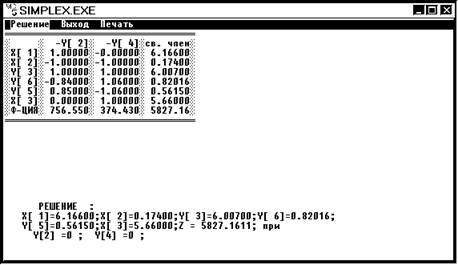
x1 = 6,166 x2 = 0,17 x3 = 5,66 Z3 = 5827,16
Вывод:
Так как на третьем шаге мы получили значения переменных равных значениям переменных на втором шаге, то мы получили искомое решение задачи нелинейного программирования. Третий шаг, за счет того, что значения коэффициента при x3 были увеличены с 40,28 до 294,68, улучшил целевую функцию Z3 на 5827,16 – 4387,26 = 1439,9 у.е.
Плановые задания предприятиям.
, где P – плановое задание тыс. тонн,q – производительность состава,x – количество составов,i – номер предприятия.
Для предприятия 1:
тыс. тонн;
Для предприятия 2: