Реферат: Изучение тригонометрического материала в школьном курсе математики

и т.д.

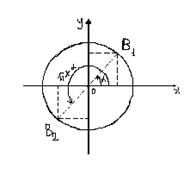
К функциям от углов можно прийти и из геометрических соображений.

Формулы приведения для и выводится из определения этих функций и ранее полученных формул приведения для синуса и косинуса. После этого полученные результаты сводятся в одну таблицу, с помощью которой можно сформулировать мнемоническое правило. Желательно учащимся предложить алгоритм применения формул приведения. Поясним его на примере:

{определяем четность, в которой оканчивается угол - II четверть; определяем знак данной функции в этой четверти – " - ". Изменяется ли название функции – нет, поэтому:} = - cos .

Вернёмся к выводу формулы синуса суммы и разности двух углов.

,

а затем применяется уже известная формула.

Формулы двойного угла выводятся из формулы синуса и косинуса суммы и разности двух углов, положив .

Сумму и разность тригонометрических функций можно преобразовать в произведение, используя следующий пример:

={ , }=

=,

но:

Таким образом:

Замечание: при ознакомлении учащихся с формулами следует добиваться от них проговаривания словесных формулировок доказываемых формул.

Наприме?