Реферат: Кинематика
![]() (2.2)
(2.2)
Так как точки А и В взяты произвольно, то все выводы справедливы для всех точек тела.
Следовательно, при поступательном движении тела его можно считать точкой и пользоваться формулами кинематики точки.
2.2 Вращение тела вокруг неподвижной оси
Вращательным называется такое движение тела, при котором хотя бы две точки, принадлежащие телу или жестко с ним связанные, во все время движения остаются неподвижными. Прямая, проходящая через эти две неподвижные точки называется осью вращения.
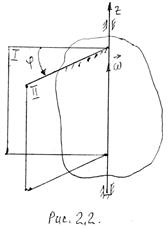
Проведем через ось вращения две полуплоскости: неподвижную І и подвижную II, жестко связанную с телом и вращающуюся вместе с ним (рис. 2.2).
Положением тела будет однозначно определяться углом φ между этими полуплоскостями. Угол φ называется углом поворота. Измеряется он в радианах. Положительное направление φ – против часовой стрелки, если смотреть навстречу оси Z .
Зависимость
φ = φ(t) (2.3)
называется уравнением вращательного движения.
|
Быстрота вращения характеризуется угловой скоростью ω . Средняя угловая скорость определяется как отношения приращения угла поворота ∆φ к промежутку времени ∆t , за который оно произошло.
![]()
Угловая скорость в данный момент времени:
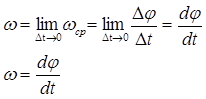 (2.3)
(2.3)
Вектор угловой скорости ![]() направлен по оси вращения в ту сторону, чтобы, глядя навстречу ему, мы видели вращение происходящей против часовой стрелки. Изменяется ω в радиан/сек. На производстве угловую скорость измеряют в об/мин. В этом случае она обозначается буквой «п».
направлен по оси вращения в ту сторону, чтобы, глядя навстречу ему, мы видели вращение происходящей против часовой стрелки. Изменяется ω в радиан/сек. На производстве угловую скорость измеряют в об/мин. В этом случае она обозначается буквой «п».
Формула перехода:
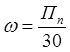 (2.4)
(2.4)
Изменение угловой скорости характеризуется угловым ускорением ε , которая определяется как первая производная от угловой скорости или вторая производная от угла поворота по времени:
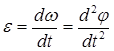 (2.5)
(2.5)
Направлен вектор ![]() также по оси вращения в сторону
также по оси вращения в сторону ![]() при ускоренном и противоположном
при ускоренном и противоположном ![]() при замедленном вращении. Единица измерения – 1Рад/с2 .
при замедленном вращении. Единица измерения – 1Рад/с2 .
2.3 Равномерное и равнопеременное вращение
Вращение называется равномерным, если угловая скорость постоянна, т.е. ω = const .
Закон равномерного вращения:
φ=φ0 +ωt (2.6)
Вращение называется равнопеременным, если угловое ускорение постоянно, т.е. ε = const .
Но ![]() . Разделяя переменные и интеграции
. Разделяя переменные и интеграции 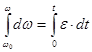 находим, что
находим, что
![]() (2.7)
(2.7)
Подставив сюда ![]() и еще раз интегрируя
и еще раз интегрируя 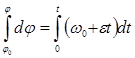 , получим уравнение переменного вращения:
, получим уравнение переменного вращения:
![]() (2.8)
(2.8)