Реферат: Кинематика

Рассмотрим переносное вращательное движение. Пусть подвижная система вращается вокруг оси О3 с угловой скоростью (рис. 3.2). единичные орты можно рассматривать как радиус-векторы точек А , В и С соответственно. А производные по времени от радиус-векторов точек дают скорости точек.

Следовательно:

; ; (а )

с другой стороны, скорости точек А, В и С мы можем найти как во вращательном движении по формуле (2.11):

; ; (б )

сравнивая (а ) и (б ) находим, что:

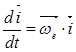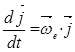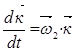; ; ;(в )

Подставим эти значения в формулу (3.7)

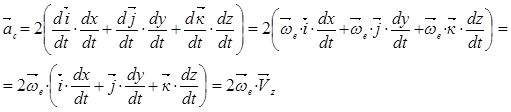
Таким образом ускорение Кориолиса равно удвоенному векторному произведению вектора угловой скорости переносного движения на вектор относительной скорости.

(3.10)

Его величина

(3.11)

В соответствии с правилом векторного произведения ускорения Кориолиса направлено перпендикулярно плоскости, в которой лежат векторы и , в ту сторону, чтобы, глядя навстречу ему, мы видим поворот вектора к вектору на меньший угол происходящим против часовой стрелки.

Другое правило: чтобы найти направление ускорения Кориолиса, надо вектор спроецировать на плоскость, перпендикулярно оси переносного вращения, и полученную проекцию повернуть на 90^о в сторону вращения. Эти и будет направление вектора .

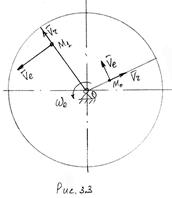
Физический смысл ускорения Кориолиса выясним на таком примере. Пусть круглая платформа вращается с постоянной угловой скоростью , а по радиусу платформы двигается точка М с постоянной относительной скоростью V _ч (рис. 3.3). В некоторый момент точка занимает положение М_о ,а через промежуток времени положение М_1. При этом произошло изменение относительной скорости за счет переносного движения (изменилось направление вектора ) и изменение переносной скорости за счет относительного движения (изменилась величина в результате удаления точки от оси вращения). Эти два изменения и характеризуются ускорением Кориолиса.

Таким образом, ускорение Кориолиса характеризует изменение относительной скорости в результате переносного движения и изменение переносной скорости в результате относительного движения.

В общем случае движения формулы (3.8) удобнее использовать в таком виде:

(3.12)

Задача кинематики плоского движения твердого тела - найти характеристики движения самого тела и отдельных его точек. В данном задании к таким характеристикам относятся векторы угловой скорости и углового ускорения тела.

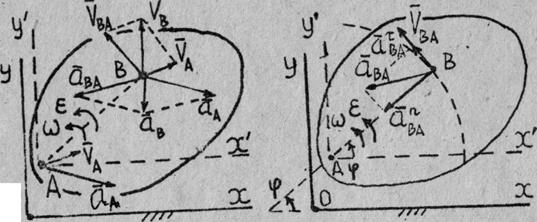
Рис. 1

Основные формулы кинематики плоского движения твердого тела - векторные формулы, связывающие соответственно скорости и ускорения двух произвольных точек плоской фигуры, например, точек А и В (рис. 1)

_B = _A + _BA = _A + ´;(1)

_B = _A + + = _A + × (´) + × ;(2)

где , , - векторы угловой скорости и углового ускорения вращения плоской фигуры вокруг любой оси, например Az' перпендикулярной плоскости движения Oxy относительно системы координат Ax'y'z', оси которой параллельны осям неподвижной системы координат Оxyz.На рис.1 оси Оz. и Аz' не изображены, так как считается, что они перпендикулярны к плоскости рисунка и направлены на наблюдателя, а плоскости Охy и Аx'y' совпадают с плоскостью рисунка.

Левые части выражений

_BA = ´; = × (´) = × _BA ; = × ;

являются соответственно векторамискорости, нормального и касательного ускорения точки В относительно системы координат Ax'y'z'при вращении отрезка АВ в плоскости рисунка вокруг точки A, называемой в таком случае полюсом, с угловой скоростью и угловым ускорением . Индексы n и t , в выражениях и указывают, что эти векторы направлены соответственно по внутренней нормали и касательной в точке Bк окружности радиуса r = AB с центром в точке А. Модули упомянутых векторов находятся по формулам