Реферат: Кольца и полукольца частных

Определение ₄ . Будем писать если и согласованы на пересечении своих областей определений, т.е. для .

Лемма 1. тогда и только тогда, когда и согласованы на некотором плотном идеале.

Доказательство.

Если то и согласованы на . По свойству 3⁰ идеал является плотным. Следовательно, и согласованы на плотном идеале.

Обратно, пусть и согласованы на плотном идеале . Тогда если и , то отсюда в силу плотности идеала , для , но это равенство выполняется тогда, когда пересечением областей определений и является отсюда следует, что .▲

Лемма 2. Отношение является конгруэнцией на системе .

Доказательство.

Для того чтобы доказать, что - конгруэнция, нужно показать:

1. отношение - рефлексивно, симметрично, транзитивно.

Рефлективность: и согласованы на плотном идеале .

Симметричность: пусть , т.е. и согласованы на .

Транзитивность: пусть и , т.е. и согласованы на плотном идеале

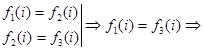
и согласованы на плотном идеале . Значит и согласованы на идеале , являющемся плотным , и согласована с на , тогда согласована с на плотном идеале по Лемме 1

Таким образом, - отношение эквивалентности.

2. отношение сохраняет полукольцевые операции.

- Пусть и , т.е. для и для .

Тогда и определены и согласованы на плотном идеале отсюда по Лемме 1 .

- Пусть и , т.е. для и для .

Тогда и определены и согласованы на плотном идеале отсюда по Лемме 1 .▲

Теорема₂ . Если - коммутативное полукольцо то система так же является коммутативным полукольцом. . (Будем называть полным полукольцом частных полукольца )

Доказательство.

- разбивает множество дробей на непересекающихся классов эквивалентности.

По Лемме 2 все тождества выполняющиеся в справедливы и в .

Чтобы убедится, что коммутативное полукольцо остаётся проверить справедливость законов дистрибутивности и коммутативности.

1. Дистрибутивность.

Отображения: и согласованы на идеале покажем, что образы отображений и совпадают на этом идеале:

пусть , где .

Тогда .

Областью определения является . По определению идеала: то для , а идеал (свойство 3⁰ ) то: . Тогда по определению сложения отсюда следует . Покажем . По определению