Поэтому, гомоморфизм является мономорфизмом и вкладывается в полное полукольцо частных.

Гомоморфизм будем называть каноническим мономорфизмом в .▲

Глава 3.

Определение₅ . Любому мультипликативно сокращаемому элементу сопоставим плотный идеал . Если , то элемент назовём классической дробью, полагая для .

Теорема₃ . Множество дробей образует подполукольцо полного полукольца частных, изоморфное классическому полукольцу частных полукольца .

Доказательство:

Рассмотрим отображение , т.е. .

1. Докажем, что - отображение: если и , , где , , то .

Имеем

Возьмём элемент из пересечения плотных идеалов , т.е. и

Тогда 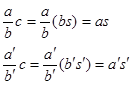, домножим на получим . Так как и на выполняется коммутативность по умножению, то , отсюда для .

2. Докажем, что является полукольцевым гомоморфизмом, т.е. сохраняются полукольцевые операции.

2.1

. Покажем, что дробь согласована с на плотном идеале .

Пусть , .

для .

Следовательно .

2.2

.

Идеал содержит , покажем, что и согласованы на плотном идеале .

Пусть , . Тогда

для .

Значит .

Таким образом - полукольцевой гомоморфизм классического полукольца частных в полное полукольцо частных .

3. Докажем, что - инъективный гомоморфизм.

Пусть для . Предположим, что дроби и согласованы на некотором плотном идеале , т.е. для выполнено . Но , . Тогда . Домножим обе части равенства на получим: