Реферат: Кольца и полукольца частных

Тогда:

Таким образом, где . По свойству 3⁰ - плотный идеал значит и согласованы на плотном идеале .

2. Коммутативность.

Отображения и согласованы на плотном идеале докажем что их образы совпадают на этом идеале: .

Доказано ранее, что пусть элементы тогда

Отсюда следует, что и согласованы на плотном идеале .

Таким образом, по Лемме 1.

Наконец сопоставим дробь: с областью определения при которой переходит в .

Предложение₂ . Отображение является гомоморфизмом т.е. сохраняет операции:

Доказательство:

1. Пусть , и где и .

Нужно показать, что . Покажем равенство образов и .

Рассмотрим дробь , такую что

для . (1)

С другой стороны рассмотрим дроби и , такие что для . (2)

Из (1) и (2) следует, что .

По свойству сложения смежных классов:

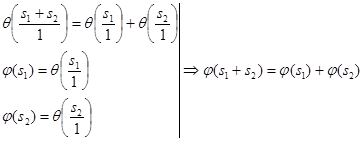для

2. Пусть , и где и .

Нужно показать, что . Покажем равенство образов и .

Рассмотрим дробь , такую что

для . (3)

С другой стороны рассмотрим дроби и , такие что для . (4)

Из (3) и (4) следует, что .

По свойству умножения смежных классов:

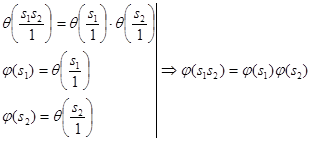для .

Таким образом гомоморфизм.

Пусть , тогда