Реферат: Курс лекций по теории вероятностей
Число благоприятных исходов равно произведению (по теореме 1) числа способов выбрать k 1 белых шаров из n 1 и числа способов выбрать k -k 1 черных шаров из n -n 1 :
![]()
??????????? ??????? A ?????:
2. Выбор с учетом порядка. Общее число элементарных исходов есть число способов разместить n элементов на k местах![]() (по теореме 2).
(по теореме 2).
??? ???????? ????? ????????????? ??????? ????? ??????, ??? ????? ???????? ??????? ?????? ????? ?????, ??? ? ????? ???????? ??????????? ??? ???? ????? k . ?????, ??????, ????????? ????? ???????? ??????? k 1 ???? ????? k (??????
? ????????????? ?????? ?? ??????????? ??????? ?????? ?? k 1 ????? ? k - k 1 ?????? ????? ??????????? ???????? ???? ????? ??? ?????? k ????? ?? ????, ?????????? n 1 ????? ? n - n 1 ?????? ?????:
Определение 8 . ???????????? ??? ????????? ????? ????????????
Называется гипергеометрическим распределением .
Раздел 2. Геометрическая вероятность
2.1 Что это такое
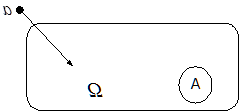 Рассмотрим какую-нибудь область Ω в Rm ,(на прямой, на плоскости, в пространстве). Предположим, что «мера» Ω (длина, площадь, объем, соответственно) конечна. Пусть случайный эксперимент состоит в том, что мы наудачу бросаем в эту область точку а . Термин «наудачу» здесь означает, что вероятность попадания точки в любую часть А ÍΩ не зависит от формы или расположения А внутри Ω , а зависит лишь от «меры» области.
Рассмотрим какую-нибудь область Ω в Rm ,(на прямой, на плоскости, в пространстве). Предположим, что «мера» Ω (длина, площадь, объем, соответственно) конечна. Пусть случайный эксперимент состоит в том, что мы наудачу бросаем в эту область точку а . Термин «наудачу» здесь означает, что вероятность попадания точки в любую часть А ÍΩ не зависит от формы или расположения А внутри Ω , а зависит лишь от «меры» области.
Определение 9 . ??????????? ????????????? ???????? ???????????????? ??????????? ????????????, ???? ??? ?????? можно ?????????? ??????? ????????? ??????? Ω ? Rm ???, ??? ??????????? ????????? ????? ? ????? А ÍΩ ?? ??????? ?? ????? ??? ???????????? А ?????? Ω , ? ??????? ???? ?? ???? ??????? А (?, ?????????????, ??????????????? ???? ????):
«Мерой» мы пока будем называть длину, площадь, объем и т.д.
Если для точки, брошенной в область Ω , выполнены условия геометрического определения вероятности, то говорят, что точка равномерно распределена в области Ω.
Пример 8 . Точка наудачу бросается на отрезок [0,1]. Вероятность точке попасть в точку {0,5} равна нулю, так как мера множества, состоящего из одной точки («длина точки»), есть 0. Вместе с тем попадание в точку {0,5} не является невозможным событием — это один из элементарных исходов эксперимента.
2.2 Задача о встрече
Пример 9 . Два лица Х и У условились встретиться в определенном месте между двумя и тремя часами дня. Пришедший первым ждет другого в течении 10 минут, после чего уходит. Чему равна вероятность встречи этих лиц, если каждый из них может прийти в любое время в течение указанного часа независимо от другого?
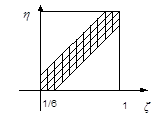 |
????? ??????? ???????? ? 14 ?? 15 ????? ??? ???????? [0,1] ?????? 1 ???. ????? ξ (?????) ? η (?????) ? ??????? ??????? Х ? У (????? ??????? [0,1]).??? ????????? ?????????? ???????????? ? ????????? ????? ???????? ?? ???????? 1:
Ω = {( ξ , η): 0 £ ξ £ 1 0 £ η £ 1 }=[0,1] x[0,1]
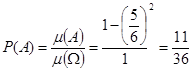 |
????? ???????, ??? ??????????? ???????? ? ???????? ????? ??????? ? ???????. ??? ???? ?????????????? ???????? ???????? ????? ????????? A = {( ξ , η): │ξ - η│ £ 1/6 } (10 ????? = 1/6 ????). ?? ???? ????????? ? ????????? A ??????? ????????? ? ??????? ????? ????????, ??? Х ? У ??????????.
Тогда вероятность встреч и равна
2.3 Задача Бюффона
Пример 10 . На плоскости начерчены параллельные прямые, находящиеся друг от друга на расстоянии 2 a . На плоскость наудачу брошена игла длины 2 l < 2 a . Какова вероятность того, что игла пересечет одну из прямых?
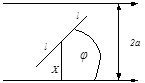 Поймем, что означает здесь «наудачу брошена игла». Возможные положения иглы (отрезка) на плоскости полностью определяются положением середины иглы и углом поворота иглы относительно какого-либо направления. Причем две эти переменные (положение центра и угол поворота) меняются независимо друг от друга. Обозначим через х Î [0, a ] расстояние от середины иглы до ближайшей прямой, аφ Î [0, π ] —
Поймем, что означает здесь «наудачу брошена игла». Возможные положения иглы (отрезка) на плоскости полностью определяются положением середины иглы и углом поворота иглы относительно какого-либо направления. Причем две эти переменные (положение центра и угол поворота) меняются независимо друг от друга. Обозначим через х Î [0, a ] расстояние от середины иглы до ближайшей прямой, аφ Î [0, π ] —
угол между каким-то направлением прямых и иглой. Множество возможных положений иглы целиком определяется выбором наудачу точки из прямоугольника Ω = [0, π ] x[0, a ] . Игла пересекает ближайшую прямую, если координаты выбранной наудачу точки удовлетворяют неравенству: х £ . l sin φ
??????? ??????? А Í Ω , ????? ??????? ????????????? ?????? ???????????, ?????
? ??? ??? μ(Ω) = a π , ?? ??????? ??????????? ?????
2.4 Парадокс Бертрана
Пример 11 ( Josef Bertrand, “Calcul des Probabilites", 1888).
В круге единичного радиуса наудачу выбирается хорда. Какова вероятность того, что ее длина будет больше, чем длина стороны вписанного в круг правильного треугольника?
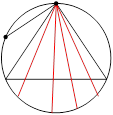 Есть по крайней мере три способа «выбрать наудачу хорду в круге». 1. Зафиксируем одну точку (конец хорды) на окружности и выберем наудачу на окружности другую точку (второй конец хорды). Здесь Ω = [0, 2π] , а благоприятными являются положения второй точки на интервале [2π/3, 4π/3] (хорды, помеченные на рисунке красным цветом). Вероятность получить «длинную» хорду равна 1/3.
Есть по крайней мере три способа «выбрать наудачу хорду в круге». 1. Зафиксируем одну точку (конец хорды) на окружности и выберем наудачу на окружности другую точку (второй конец хорды). Здесь Ω = [0, 2π] , а благоприятными являются положения второй точки на интервале [2π/3, 4π/3] (хорды, помеченные на рисунке красным цветом). Вероятность получить «длинную» хорду равна 1/3.
 2. Существует ровно одна хорда, для которой данная точка в круге является серединой (кроме того случая, когда брошенная наудачу точка попадет в центр круга. Но поскольку вероятность этого события равна нулю, то учет или неучет такого события не влияет на итоговую вероятность). Можно поэтому выбирать наудачу хорду, бросая наудачу точку (середину хорды) в круг. Здесь Ω — круг радиуса 1, μ(Ω) = π , а благоприятными являются положения середины хорды внутри вписанного в треугольник круга (радиусом 1/2).Вероятность получить «длинную» хорду равна отношению площадей кругов, то есть 1/4.
2. Существует ровно одна хорда, для которой данная точка в круге является серединой (кроме того случая, когда брошенная наудачу точка попадет в центр круга. Но поскольку вероятность этого события равна нулю, то учет или неучет такого события не влияет на итоговую вероятность). Можно поэтому выбирать наудачу хорду, бросая наудачу точку (середину хорды) в круг. Здесь Ω — круг радиуса 1, μ(Ω) = π , а благоприятными являются положения середины хорды внутри вписанного в треугольник круга (радиусом 1/2).Вероятность получить «длинную» хорду равна отношению площадей кругов, то есть 1/4.

3. Наконец, можно ограничиться рассмотрением только хорд, перпендикулярных какому-либо диаметру (остальные могут быть получены поворотом). То есть эксперимент может состоять в выборе середины хорды наудачу на диаметре круга — отрезке длиной 2. Благоприятными являются положения середины хорды на отрезке длиной 1. Искомая вероятность для такого эксперимента равна 1/2.
В чем причина разницы в ответах на, казалось бы, один и тот же вопрос? На самом деле формулировка задач и не корректна с математической точки зрения. «Выбор наудачу хорды в круге» может быть по-разному описан с помощью геометрического определения вероятности (что мы и сделали). То есть этот «эксперимент» можно по-разному описать с помощью выбора наудачу точки в некоторой области.
Слово «эксперимент» взято в кавычки не напрасно: сказав «в круге наудачу выбирается хорда», мы еще не описали физического эксперимента. Действительно, каждому из трех предложенных способов выбора хорд можно сопоставить конкретный физический эксперимент (всякий раз другой).
Так что парадокс исчезает сразу, как только получен ответ на вопрос: что значит «в круге наудачу выбирается хорда»?
Заканчивая обсуждение понятия геометрической вероятности, сделаем очень важное для дальнейшего замечание.