Реферат: Квантово-химические правила отбора элементарных стадий
Любая термодинамически разрешенная реакция, в которой происходит незначительное перемещение ядер (близость минимумов энергетических термов) и мало изменяются электронные состояния (принцип наименьшего движения), и молекулярность которой не превышает 2, имеет шанс быть согласованным процессом, элементарной стадией. Однако, для того, чтобы величина 
была небольшой и реакция протекала с измеряемой скоростью, необходимо выполнение двух требований, вытекающих из квантово-химической теории. Эффективное взаимодействие двух частиц с достаточно низкой величиной барьера может происходить в случае, когда симметрия перекрывающихся молекулярных орбиталей (МО) будет одинаковой, а энергии этих МО будут близки. Например, бимолекулярная реакция (27)
H2 + I2 = 2HI (27)
с небольшим изменением координат ядер и валентных оболочек не является элементарным процессом (ЭС), поскольку запрещена по симметрии граничных МО. Рассмотрим подробнее некоторые квантово-химические подходы к проблеме реакционной способности.
Теория возмущений в приближении граничных МО
Из правила БЭП следует, что знание энергетического состояния исходных и конечных продуктов позволяет оценивать кинетические характеристики ЭС (вероятность реализации элементарного акта). Метод возмущения МО (МВМО), оперируя только граничными занятыми и свободными МО (ВЗМО, НСМО) и зарядами (на атомах в молекулах и на атомных орбиталях в МО) в исходных реагентах, позволяет в ряде случаев предсказать вероятность, направление и эффективность взаимодействия двух реагентов.
Чем эффективнее взаимодействие, тем ниже Еакт и тем выше вероятность согласованного (элементарного) акта.
Если энергии граничных орбиталей c 1 и c 2 близки, то энергия взаимодействия определяется резонансным (обменным) интегралом b 12
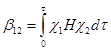(28)
где H – гамильтониан системы, t – элемент объема, в котором происходит перекрывание орбиталей. Величина b 12 в этом случае определяет и величину расщепления новых МО Y 1 и Y 2 или энергию стабилизации e = b 12 .
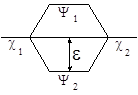
Если энергии c 1 и c 2 различаются сильно, то величина e определяется не только b 12 , а зависит и от разности энергий c 1 и c 2 по уравнению (29):
(29)
где Е 1 и Е 2 – энергии низшей и высшей МО
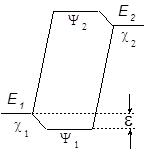
Чем больше величина e , тем стабильнее образующийся аддукт, тем ниже Еакт его образования.
МВМО не дает оценки Е переходного состояния и Еакт . Рассчитывается лишь разница между полной электронной энергией реагирующей системы Е и энергиями исходных реагентов 
и 
(малое возмущение):
DЕ = Е – – , (30)
справедливое только для начальных участков координаты реакции. Только на больших расстояниях между реагентами не происходит смешения МО, нет межмолекулярного отталкивания и можно говорить о чистых МО исходных реагентов. Вместе с тем, такое приближение позволяет оценить наиболее вероятный путь реакции.
Энергию возмущения DЕ при взаимодействии реагентов S и Т (S и Т – молекулы или активные центры в молекулах) рассчитывают по уравнению 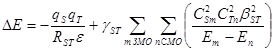(31):
(31)
В случае только двух граничных МО (например, молекул донора и акцептора) уравнение упрощается 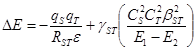(32):
(32)
В уравнениях (31, 32) qS и qT – эффективные заряды на центрах S и Т , RST – расстояние между центрами в ходе взаимодействия, e – диэлектрическая проницаемость среды. Таким образом, первый член (возмущение 1го порядка) отражает энергию кулоновского взаимодействия. Второй член (возмущение 2го порядка) определяет энергию орбитального перекрывания и включает: g ST – коэффициент, учитывающий заселенность электронами орбиталей c 1 и c 2 , 
и 
– квадраты коэффициентов при атомных орбиталях центров S и Т волновой функции граничных МО c 1 и c 2 , 
– квадрат обменного интеграла, Е 1 и Е 2 – энергии орбиталей c 1 и c 2 . Разные случаи заселенности орбиталей c 1 и c 2 реагирующих частиц и коэффициент g ST приведены ниже:
|
Число электронов на |
g ST |
|
2 + 2, 0 + 0 |
0 (нет перекрывания) |
|
2 + 1, 1 + 0 |
1 |
|
2 + 0, 1 + 1 |
--> ЧИТАТЬ ПОЛНОСТЬЮ <-- К-во Просмотров: 304
Бесплатно скачать Реферат: Квантово-химические правила отбора элементарных стадий
|