Реферат: Л. И. Мандельштамом и Н. Д. Папалекси

Решение задач Коши (1) и (4), (3) и (4) существует и единственно. Поэтому решение (1) и (4) будем искать методом приближений.

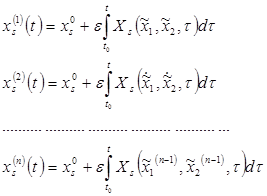
Обозначим

(*)

Функция — 2-периодическая по .

Пусть

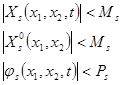(7)

удовлетворяет условиям Липшица по переменным и. Проинтегрируем функцию :

.

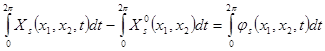Интеграл 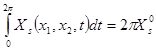и 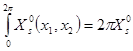поэтому

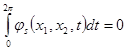
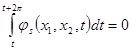(7a)

В промежутке находятся те значения t, для которых будет существовать решение (1) - (4) и оно не выйдет за пределы области G. Это характеризуется так

Из теоремы Пикара следует, что при всех таких t приближенное выражение сходится к решению задачи Коши:

— целую часть от деления обозначим N. Тогда — дробная часть

,

где — остаточный интервал.

С учетом возможности такого разбиения

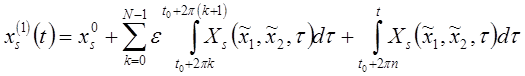
Если рассмотреть , то последнее выражение перепишется в виде:

=,

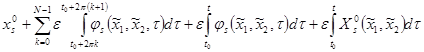где с учетом (4)

=

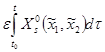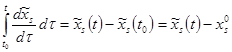
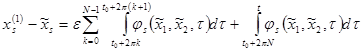
Рассмотрим интеграл при

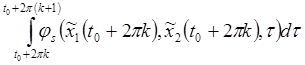
и от не зависят. Из равенств (7а) следует, что последнее выражение равно нулю .

Вычислим

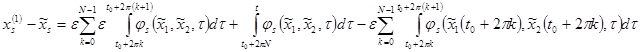
То есть

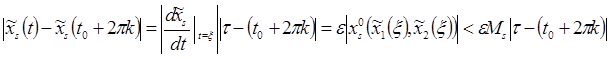
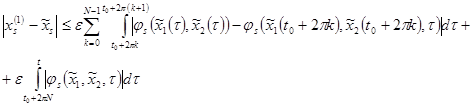(8)

Мы можем сказать, что в (8), все, что стоит под знаком суммы

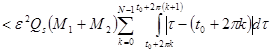
Так как

,

то последнее неравенство равносильно следующему:

Поэтому:

=, (9)