Реферат: Л. И. Мандельштамом и Н. Д. Папалекси

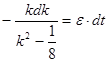
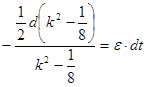
Так как ,

то тогда ,

или

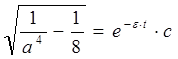
Предположим, что , тогда

; ;

+.

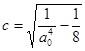
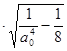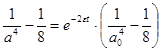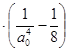Отсюда находим

(9а)

Колебания представятся следующим образом (находим выражение для приближенного значения x в явном виде)

(9)

Найдем

Динамический режим обладает сильной устойчивостью, заключающейся в том, что каково бы ни было значение , малое или большое, все равно при .

Как видно из выражения (9), если начальное значение амплитуды =0, амплитуда останется равной нулю для любого t, и, следовательно, получим х=0, то есть тривиальное решение уравнения (1). Это тривиальное решение, очевидно, соответствует статическому режиму, то есть отсутствию колебаний в системе.

Однако, исходя из формулы (9), нетрудно заключить, что этот статический режим неустойчив. Действительно, как бы ни было мало начальное значение амплитуды, оно все равно будет монотонно приближаться к значениям, равным . Таким образом, поскольку случайные малые толчки практически неизбежны, в рассматриваемой колебательной системе, находящейся в состоянии покоя, автоматически возбуждаются колебания с амплитудой, то есть система самовозбуждается.

Из выражения (9) следует, что если , то , и для любых очень быстро приближается к значению независимо от . Это решение соответствует стационарному (установившемуся) динамическому режиму:

(10)

Иначе говоря, любое колебание при увеличении t приближается к стационарному колебанию, то есть колебания будут устойчивы.

Режимы с постоянной амплитудой, для , приводят к уравнению

А==0

.

Корни этого уравнения ;

; <0

Таким образом, соответствует неустойчивому состоянию равновесия, а соответствует устойчивому предельному циклу.

Для любого заданного положительного сколь угодно малого значения параметра всегда можно найти такое достаточно малое значение параметра , для которого уравнение (1) или, что то же самое, система (2), имела бы предельный цикл, лежащий в окрестности окружности , причем этот предельный цикл устойчив, если, и неустойчив, если . Все эти рассуждения следуют из теоремы Мандельштама и Папалекси.

Наряду с точной системой рассматривается приближенная

, (s=1,2) .

Теорема. Пусть при всех t и в некоторой области переменных функции непрерывны и ограничены. Функции также непрерывны и ограничены в области Г. — 2-периодические по t. Функции и — удовлетворяют условию Липшица по переменным и (при этих условиях существует и единственно решение). Тогда для и L>0 : , 0,

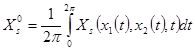
где (s=1,2) =

(s=1,2)