Реферат: Лекции по математической статистике

Даже при наилучшем линейном предсказании, предсказание будет отличаться от реального y_i на какую-то величину, которую мы назовем ошибкой оценки и обозначим e_i :

Точность предсказания зависит от того, насколько удачно подобраны коэффициента b ₁ и b ₀ . Критерием успешности подбора коэффициентов является минимальная величина суммы квадратов всех ошибок оценки – критерий наименьших квадратов

Другой критерий: . Этот критерий приводит к медианой линии регрессии. Из уравнения следует

Исходя из минимизации формулы наименьших квадратов найдем формулы:

;

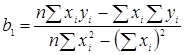Наше исследование получается наиболее результативным, если мы предполагаем, что фактор и отклик имеют двумерные нормальные распределения.

Свойства двумерного нормального распределени я

1. Выборочные средние отклика (y ) для каждого значения x лежат на прямой;

2. Для любого значения x , соответствующие значения y нормально распределены;

3. Для любого значенияx , y – имеют одинаковую дисперсию .

При прогнозировании является ли среднее ошибок оценки подходящей мерой для прогнозирования.

Средняя ошибка оценки всегда равна нулю. Один из способов доказать этот факт, это выбрать в качестве меры прогнозирования дисперсию ошибки оценки.

Стандартная ошибка оценки

Стандартную ошибку оценки применяют для определения пределов, в окрестности предсказанного попадает фактическое значение y_i .

В приделах S_e – расположено 69% фактических значений объекта, в приделах 2S_e – 95%, в приделах 3S_e – 97,5%.

Связь b ₁ и b ₀ с другими описательными статистиками

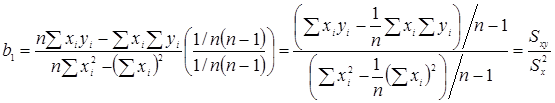
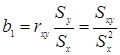
Если x и y распределены по нормальному закону и имеют одинаковую дисперсию, то .

Поскольку r_xy не зависит от S_x и S_y , b ₁ - принимает максимальное значение при r_xy =1 и минимальное значение при r_xy = -1, следовательно b ₁ никогда не может быть больше , при r_xy =1 и не может быть меньше при r_xy = -1.

Если между переменными отсутствует линейная связь, b ₁ =0 уравнение регрессии сводится к прямой без наклона, то есть .

Измерение нелинейной связи между переменными

Для определения меры нелинейной связи между переменными используется коэффициент

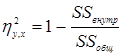
Эта мера может быть использована и для оценки линейной связи.

Пример вычисления:

x/возраст	10	14	18	22	26	30	34	38
7	8	9	11	9	8	7	8
8	9	10	11	10	9	9
9	10	11	12	11	9	10
9	11	12	12	10
10

Находим среднее для каждого возраста и суммируем отношения каждого y_i от среднего соответствующего группы.

Для 10 - =8,6; 18 – 9,5; 22 – 11,5; 26 – 10; 90 – 9; 34 – 8,67; 38 – 8.