Реферат: Лекции по математической статистике

- является мерой нелинейности связи и

Другие меры связи

1. Измерения в дихотомической шкале (например, женат – не женат, мужчина – женщина)

2. Измерение в дихотомической шкале наименований в предположении нормального распределения. Предполагается, что при более полных, более совершенных измерениях данные распределятся по нормальному закону.

3. Шкала порядка

4. Измерение в шкале интервалов или отношений.

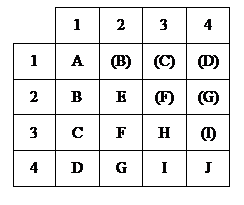Рассмотренный ранее коэффициент кореляции Пирсона соответствует сочетанию J при измерении исходных данных. Для описания степени кореляции при других комбинациях шкал измерений исходных данных используются следующие меры.

Случай A .

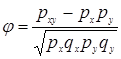
p_x – доля людей имеющих 1 по x, p_y – доля людей имеющих 1 по y

q_x – доля людей имеющих 0 по x, q_y – доля людей имеющих 0 по y

p_xy - доля людей имеющих 1 по x и y

№	1	2	3	4	5	6	7	8	9	10	11	12
x	0	1	0	0	1	1	0	1	0	0	0	1
y	0	1	1	0	1	0	0	1	0	1	0	1

x – женат / холост

y – исключенные из учебного заведения / оставшиеся

p_x =0,4167 ; p_y = 0,5 ; q_x =0,5833 ; q_y = 0,5 ; p_xy =0,333; φ=0,507

Если нет особого интереса к доле p_x и p_y , дихатомические данные располагают в таблице сопряженности признаков. Пример таблицы сопряженности по приведенным данным

φ – определяется по формуле:

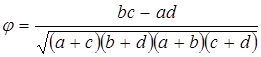
Коэффициент φ, это тот же коэффициент кореляции Пирсона, но эти данные не похожи на двумерное нормальное распределение, которое мы представляли при вычислении коэффициента Пирсона. Это рассматривается как большое неудобство статистиками.

Случай B .

Удовлетворительного коэффициента для этого случая не существует, рекомендуется исходить из предположения о нормальном распределении данных и вычис