Реферат: Математические методы и модели в экономике 2

х₁₁ +х₁₂ +х₁₃ =400

х₂₁ +х₂₂ +х₂₃ =250

, где х, х_ij – целые числа.

Задача 2

Решить графическим методом.

Решить графическим методом

Z= 3 х₁ -4х₂ → max при условиях:

-х₁ +х₂ ≤1

-х₁ +2х₂ ≥-2

х₁ +х₂ ≥-1

-3х₁ +2х₂ ≤6;

2х₁ – х₂ ≤2

х₁ ≥0; х₂ ≥0

Решение

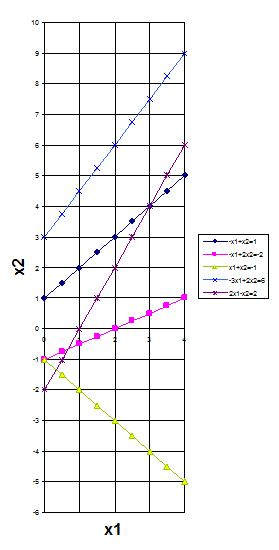
Запишем ограничения в виде равенств и построим соответствующие им линии уровня в системе координат. Строим область допустимых значений решения, удовлетворяющую начальным условиям. Семи заданным неравенствам соответствует множество точек плоскости, образующие пятиугольник АВСDE. Неравенства х₁ ≥-4; х₁ +5х₂ ≥4 могут быть исключены, так как они определяют граничные прямые, не имеющие с АВСDE общих точек.

Строим на плоскости вектор целевой функции . Через начало координат перпендикулярно проводим линию уровня целевой функции Z=0. Линия уровня перемещается в направлении параллельно самой себе, пока не встретится с вершиной области допустимых значений АВСО т. В. Значение Z в точке В является минимальным.

При дальнейшем перемещении линия уровня пройдет через другую вершину ОДР, выходя из области решений – точку С. Значение Z в точке С является максимальным. Значение целевой функции Z_{m ах} в т. С. Найдем её координаты:

2х₁ – х₂ =2

х₂ =0

С(0; 1)

Z_{m ах} =3*1-4*0=3

Ответ: Z_{m ах} =3.

С

Z

В

А

Задача 4

Удельные затраты С_ij на перевозку 1 т груза вида i транспортом j (руб.) представлены матрицей

С_ij =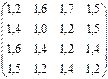

Мощности поставщиков А₁ =30 тыс.т; А₂ =10 тыс.т; А₃ =40 тыс.т; А₄ =70 тыс.т. Спрос потребителей: В₁ =30 тыс.т; В₂ =10 тыс.т; В₃ =20 тыс.т; В₄ =10 тыс.т.

Определить объемы перевозок груза транспортом j (руб.), чтобы суммарные издержки были бы минимальными, построить матрицу объемов перевозок.

Решение

1. Определяем тип задачи. Так как 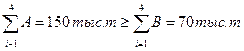. Задача является открытой. Введем фиктивного потребителя с объемом потребления В_ф .