Реферат: Математические методы и модели в экономике 2
Задача 11
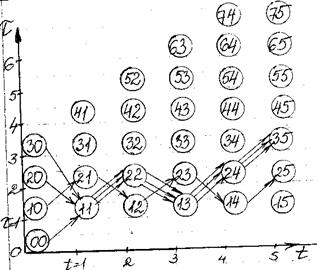
Дана схема движения транспорта с n=5 пунктами и расстояниями между ними. Построить кольцевой маршрут объезда всех пунктов наименьшей длины.
| ∞ | 13 | 12 | 11 | 7 |
| 10 | ∞ | 6 | 9 | 4 |
| 13 | 10 | ∞ | 12 | 7 |
| 9 | 6 | 14 | ∞ | 8 |
| 12 | 13 | 9 | 10 | ∞ |
Решение
Стоим приведенную матрицу с целью получения в каждой строке и столбце не меньше 1 кратчайшего маршрута (0 приведенного значения). Коэффициенты приведения
по строкам: К1 =7+4+7+6+9=33
| ∞ | 6 | 5 | 4 | 0 |
| 6 | ∞ | 2 | 5 | 0 |
| 6 | 3 | ∞ | 5 | 0 |
| 3 | 0 | 8 | ∞ | 2 |
| 3 | 4 | 0 | 1 | ∞ |
по столбцам (у приведенной матрицы): К2 =3+1=4
![]() Кпр =33+4=37 (сумма самых коротких маршрутов).
Кпр =33+4=37 (сумма самых коротких маршрутов).
| 6 | 5 | 3 | 0 | |
| 3 | ∞ | 2 | 4 | 0 |
| 3 | 3 | ∞ | 4 | 0 |
| 0 | 0 | 8 | ∞ | 2 |
| 0 | 4 | 0 | 0 | ∞ |
Для нулевых значений определяем коэффициенты значимости:
К41 =0; К51 =0; К42 =3; К53 =2; К25 =2; К15 = К35 =3; К54 =3.
Выбираем аij =0 с максимальным Кij , например, К15 =3.
В матрице назначения присваиваем Х15 =1. В полученную матрицу в клетку (5,1) вводим запрет.
![]() Приведем матрицу.
Приведем матрицу.
| 2 | 3 | 4 | 1 | |
| ∞ | 0 | 2 | 1 | |
| 3 | 0 | ∞ | 1 | 0 |
| 4 | 0 | 8 | ∞ | 0 |
| 5 | 4 | 0 | 0 | ∞ |
Подсчитаем новое значение Кпр : 37+2+3=42.
Определяем коэффициенты значимости для нулевых значений.
К32 =К42 = К53 =К41 =К31 =0; К23 = К54 =1.
Выбираем аij =0 с максимальным Кij , например, К23 =1.
В матрице назначения присваиваем Х23 =1. В полученную матрицу в клетку (3,2) вводим запрет.
| 2 | 1 | ||
| 3 | ∞ | 1 | 0 |
| 4 | 0 | ∞ | 0 |
| 4 | 0 | ∞ |
Так как матрица уже приведена, определяем коэффициенты значимости для нулевых значений.
К42 =4; К41 =0; К31 =1; К54 =5.
Присваиваем в матрице назначения Х54 =1. В полученную матрицу в клетку (4,1) вводим запрет.
| 2 | 1 | |
| 3 | ∞ | 0 |
| 4 | 0 | ∞ |
В полученной матрице осталось два маршрута, которые и вносим в кольцевой маршрут: Х31 =1; Х42 =1.
Введем все маршруты в матрицу назначения.
| 1 |
| 1 |
| 1 |
| 1 |
| 1 |
Длина полученного маршрута:
![]()
Условие оптимальности F=Кпр. =42 выполняется, то полученный кольцевой маршрут является оптимальным.
Задача 13
Рассматривается круглосуточная работа пункта проведения профилактического осмотра автомашин. Пункт состоит из n=3 каналов; на осмотр каждой машины затрачивается ![]() При осмотре группа выявляет дефект с вероятностью р=0,7; на осмотр поступает в среднем
При осмотре группа выявляет дефект с вероятностью р=0,7; на осмотр поступает в среднем ![]() . Обслуживание одной заявки приносит среднюю прибыль С1 =3 руб./час, создание 1 канала требует среднего расхода С2 =18000 тыс.р., эксплуатация 1 канал в единицу времени требует среднего расхода С3 =8 руб./час. Определить характеристики работы пункта. Установить, при каких соотношениях С1 ,С2 , С3 система будет рентабельна, и если система не рентабельна при заданных С1 ,С2 , С3 , то при каких она будет рентабельна? Через какое время эксплуатации система будет приносить прибыль?
. Обслуживание одной заявки приносит среднюю прибыль С1 =3 руб./час, создание 1 канала требует среднего расхода С2 =18000 тыс.р., эксплуатация 1 канал в единицу времени требует среднего расхода С3 =8 руб./час. Определить характеристики работы пункта. Установить, при каких соотношениях С1 ,С2 , С3 система будет рентабельна, и если система не рентабельна при заданных С1 ,С2 , С3 , то при каких она будет рентабельна? Через какое время эксплуатации система будет приносить прибыль?
Решение
Характеристики работы системы:
1. Среднее число занятых каналов