Реферат: Математична статистика

,(1.6)

яка є незміщенною (, s_z – середньоквадратичне відхилення генеральної сукупності), ефективною та умотивованною.

Статистичними оцінками ймовірностей є відносні частоти

,

які є незміщенними (), ефективними та умотивованими.

Довірчі інтервали ймовірностей обчислюються за формулами

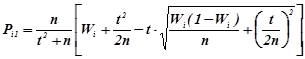,(1.7а)

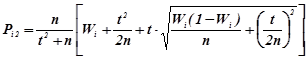.(1.7b)

Значення змінної t (різне для кожного i ) знаходиться з умови , де - інтеграл Лапласа,- надійність відносної частоти як статистичної оцінки ймовірності p_i .

Приклад 1.2. Несиметричний кубик кинули 80 разів і при цьому шість очок випало 16 разів. Знайти довірчий інтервал для невідомої ймовірності з надійністю 0.9

Розв’язування . За умовою задачі . Відносна частота .Значення змінної t знаходиться рівняння

. Розв’язок рівняння . За формулами (4.1.6а) та (4.1.6b)

,

.

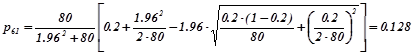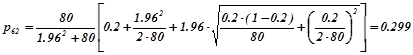Отже, довірчий інтеграл для оцінки невідомої ймовірності з надійністю 0.9

7. Метод максимальної правдоподібності

Метод максимальної провдоподібності використовуються для знаходження статистичних оцінок параметрів розподілів випадкових величин (як дискретних, розподіл яких задається аналітичним виразом, так і неперервних випадкових величин).

Нехай X – випадкова величина з розподілом (якщо вона дискретна) або густиною розподілу ймовірностей (якщо вона неперервна) , який (яка) однозначно визначається параметром, і який невідомий. Для його визначення здійснюється n експериментів. Результати кожного з експериментів є випадковими величинами . Очевидно, що розподіли цих випадкових величин співпадають з функцією випадкової величини X . Експерименти незалежні, тому за теоремою множення ймовірностей незалежних подійможна записати

.

Функція

(2.1)

називається функцією максимальної правдоподібності . Точка , в якій функція максимальної правдоподібності досягає максимуму є значенням статистичної оцінки параметра розподілу . Така статистична оцінка називається оцінкою найбільшої правдоподібності .

Функції та досягають максимуму в одинакових точках. Тому замість точки максимуму функції шукають точку максимуму функції , що значно зручніше. З математичного аналізу відомо, що точку максимума функції можна знайти за таким алгоритмом:

1) знаходять похідну і прирівнюють до нуля: ;

2) розв’язують одержане рівняння і знаходять екстремальні точки ;

3) знаходять другу похідну ; якщо друга похідна в екстремальній точці від’ємна, то така точка є точкою максимума функції, якщо додатня, то – мінімуму.

Методом максимальної правподібності одержані важливі для практики результати:

1) статистична оцінка параметра розподілу Пуассона

;(2.2)

2) статистична оцінка параметра p біноміального розподілу є