Реферат: Математична статистика

;

.

4. Стандартні розподіли математичної статистики

4.1 Розподіл (хі-квадрат )

Нехай - система нормальних випадкових величин з одинаковими математичними сподіваннями та середньоквадратичними відхиленнями . Тоді сума квадратів цих величин розподілена за законом (хі квадрат) із степенями свободи. Густина розподілу

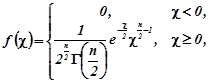(4.1.1)

де - гамма-функція (додаток 1.11).

Розподіл однозначно визначається одним параметром – числом степені свободи n . Із збільшенням числа степеней свободи розподіл повільно наближається до нормального (додаток 1.12).

Математичне сподівання та дисперсія розподілу

,

.

Доведення . За означенням математичного сподівання

,

,

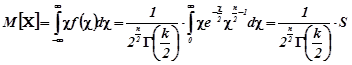(використана рівність ).

З врахуванням цього

.

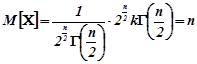Для обчислення дисперсії зручно скористатися формулою

.

За означенням математичного сподівання

,

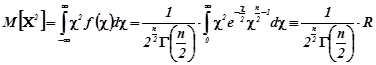З врахуванням цього

.

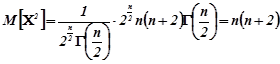
4.2 Розподіл Стьюдента

Якщо Z – нормальна випадкова величина з параметрами та , а V – незалежна від Z величина, розподілена за законом із n степенями свободи, то випадкова величина