Реферат: Математична статистика

n₁ кількість експериментів у першій серії, X₁ - кількість успіхів_; : n₂ кількість експериментів у другій серії, X₂ - кількість успіхіву другій серії;

3) статистичною оцінкою параметра експоненціального розподілу є обернена величина до вибіркового середнього:

.(2.4)

Якщо розподіл випадкової величини однозначно визначається не одним параметром, а декількома, то функція максимальної правподобності є функцією багатьох змінних:

.

В цьому випадку для знаходження точок максимуму необхідно розв’язати систему нелінійних рівнянь

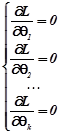(2.5)

Саме цим користуються для знаходження статистичних оцінок параметрів нормального розподіл у теорії похибок вимірювання фізичних величин.

8. Теорія похибок вимірювання фізичних величин

Кількісні результати при спостереженнях одержують, як правило, шляхом вимірювання. Якщо істинне значення деякої фізичної величини a , а в результаті вимірювання одержане значення x, то похибка вимірювання визначається як різниця між ними: . Розрізняють три види похибок: промахи, систематичні похибки та випадкові похибки.

Промахи виникають через грубе порушення умов вимірювання (неправильні дії лаборанта, несправність вимірювальної аппаратури, різка зміна зовнішніх умов) і зазвичай характеризуються порівняно великими похибками.

Систематичні похибки є результатом впливу не врахованих факторів (підвищена температура, електромагнітні завади, тощо) або недоліками вимірювальних приладів (похибка градуювання, недосконалість методу вимірювання) Промахи та систематичні похибки можуть бути виявлені і враховані як при обробці вимірювань, так і при організації вимірювань. Але як би не були добре організовані вимірювання, завжди залишається багато не врахованих факторів, вплив яких приводить до випадкових похибок .

8.1 Основна гіпотеза

Випадкові похибки є результатом дії великої кількості різних факторів , кожна з яких вносить малу похибку, і жодна з них не має домінуючого впливу (похибки зумовлені домінуючими факторами можна віднести до систематичних похибок). У відповідності до теореми Ляпунова є всі підстави вважати , що похибка є випадковою величиною D з нормальним розподілом (це суть основної гіпотези ).Ця величина може приймати значення похибки . Є також всі підстави вважати, що відхилення результатів вимірювання рівноймовірні в обидві сторони від істинного значення фізичної величини. Тому математичне сподівання випадкової похиб