Реферат: Методы исследования нелинейных систем

Представим дифференциальное уравнение 2-го порядка в виде системы

уравнений 1-го порядка:

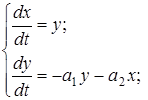(4)

где скорость изменения регулируемой величины.

В рассматриваемой линейной системе переменные x и y представляют собой фазовые координаты. Фазовый портрет строим в пространстве координат x и y, т.е. на фазовой плоскости.

Если исключим время из уравнения (1), то получим уравнение интегральных кривых или фазовых траекторий.

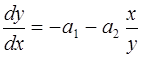. (5)

Это уравнение с разделяющимися переменными

. (6)

Рассмотрим несколько случаев

1. Пусть корни характеристического уравнения (3) имеют вид

(т.е. ). (7)

При этом переходной процесс описывается уравнениями

x = A sin (wt+j), (8)

y = Aw cos (wt+j),

т.е. представляет собой незатухающие колебания с постоянной амплитудой А и начальной фазой – j.

На фазовой плоскости (рис. 4) эти уравнения представляют собой параметрические уравнения эллипса с полуосями А и wA (где A – постоянная интегрирования).

Если обозначить

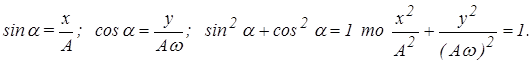
Уравнение эллипса можно получить решением уравнения фазовых траекторий

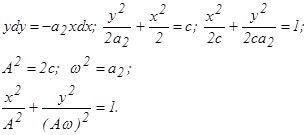(9)

Состояние равновесия определяется из условия

,

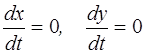при этом x₀ = y₀ = 0.

Особая точка называется "центр" и соответствует устойчивому равновесию, так как фазовые траектории от нее не удаляются.

2. Пусть корни характеристического уравнения (3) имеют вид

(10)

При этом переходной процесс описывается уравнениями:

Из уравнения фазовых траекторий получим уравнение