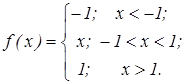Реферат: Методы исследования нелинейных систем
Пусть в области [-b, +b] система устойчива, при этом коэффициент усиления – К мал, переходный процесс затухает, особая точка "устойчивый фокус" вне области К – большой, переходный процесс расходится (рис. 22). Эта система имеет неустойчивый предельный цикл, т.е. автоколебания неустойчивы.
Для более сложных нелинейных элементов может быть несколько предельных циклов.
Пример Для заданной системы (рис. 23) построить примерный фазовый портрет.
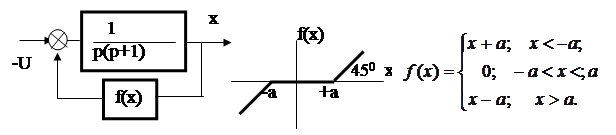
Рис. 23
Решение: Исходную схему можно представить в виде (рис. 24).
 |
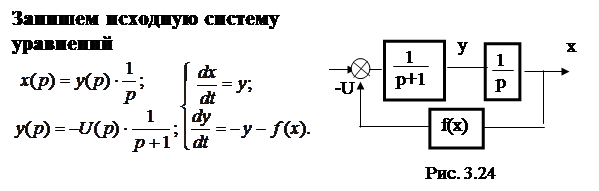Построим фазовый портрет
1) При – a < x < +a f(x) = 0, а система уравнений имеет вид
 |
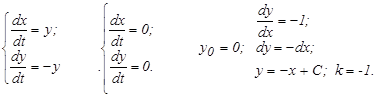
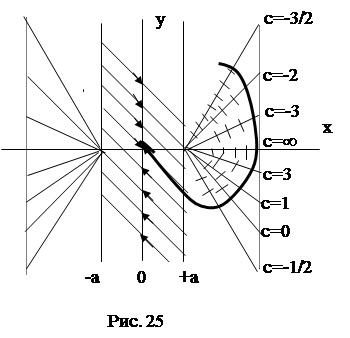Фазовый портрет в этой области представляет семейство прямых с коэффициентом к = -1, а состояние равновесия устойчиво по Ляпунову и представляет отрезок оси y = 0 на интервале – a <x < +a (рис 25).
2) При x > +a f(x) = x – a, а система уравнений имеет вид
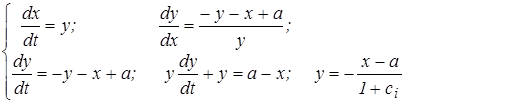
Для каждого сi определимугловой коэффициент наклона изоклины – к по формуле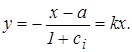 
и угол пересечения фазовой траекторией изоклины по формуле a = arctg c, результаты приведены в таблицах 1 и 2.
Таблица 1
| Сi | 0 | 1 | 2 | 3 | -1/2 | -2 | -3 | ¥ |
| k | -1 | -1/2 | -1/3 | -1/4 | -2 | 1 | 1/2 | 0 |
Таблица 2
| Ci | 0 | ±1 | ±1 | ±1 | ±1 | ±¥ |
| a | 0 | ±450 | ±630 | ±710 | ±800 | ±900 |
3) При x < – a f(x) = x + a, а система уравнений имеет вид
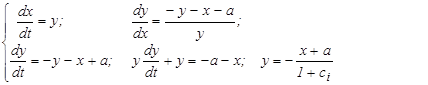
Левая часть фазового портрета строится аналогично правой.
Пример 4. Для заданной системы (рис. 26) построить примерный фазовый портрет.
 | |
|
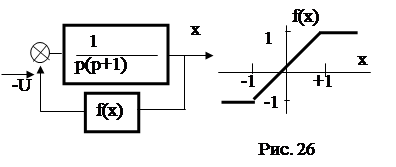Исходную схему можно представить в виде (рис. 27).
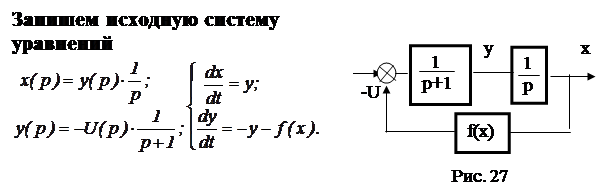
Построим фазовый портрет.
1) При –1 < x < +1 f(x) = x, а система уравнений имеет вид
 |
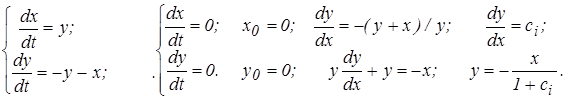
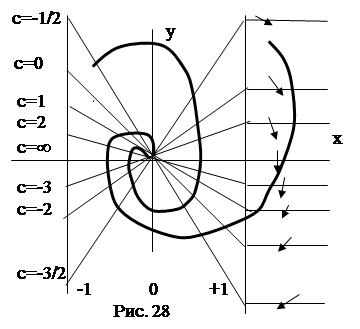Для каждого сi определимугловой коэффициент наклона изоклины – к по формуле 
и угол пересечения фазовой траекторией изоклины по формуле a = arctg c.
2) При x > +1 f(x) = 1, а система уравнений имеет вид
Для каждого сi определимугловой коэффициент наклона изоклины – к по формуле 
и угол пересечения фазовой траекторией изоклины по формуле a = arctg c.
3) При x < -1 f(x) = -1.
Левая часть фазового портрета строится аналогично правой.
Литература
1. Атабеков Г.И., Тимофеев А.Б., Купалян С.Д., Хухриков С.С. Теоретические основы электротехники (ТОЭ). Нелинейные электрические цепи. Электромагнитное поле. 5-е изд. Изд-во: ЛАНЬ, 2005. – 432 с.
2. Гаврилов Нелинейные цепи в программах схемотехнического моделирования. Изд-во: СОЛОН-ПРЕСС, 2002. – 368 с.
3. Дорф Р., Бишоп Р. Автоматика. Современные системы управления. 2002 г. – 832 с.