Реферат: Методы исследования нелинейных систем

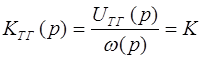. (20)

На основании функциональной схемы и полученных передаточных функций элементов системы составляем структурную схему рис. 13

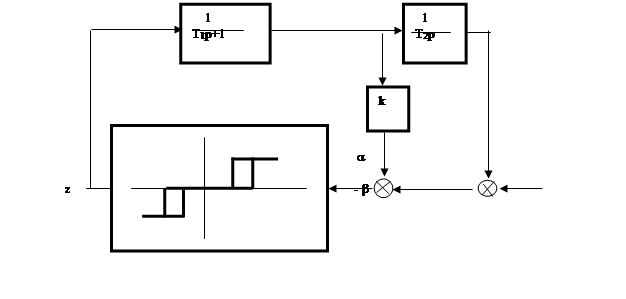
Для построения фазового портрета необходимо записать систему дифференциальных уравнений.

Рассмотрим свободное движение системы (b=0) при этом x = a.

Дифференциальное уравнение нелинейной системы имеет вид

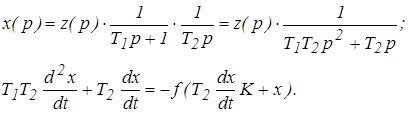(21)

Представим уравнение в виде системы уравнений:

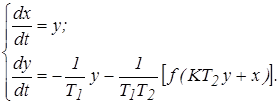(22)

Построим фазовый портрет. Для простоты построения фазового портрета делаем некоторые упрощения:

1) Пусть обратная связь по скорости – отсутствует (К = 0).

2) Характеристика нелинейного элемента однозначна (рис. 14).

При этом:

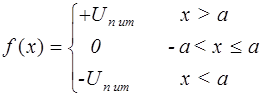(23)

С учетом принятых допущений система уравнений упрощается.

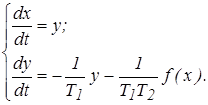(24)

Построим характеристику для каждой зоны.

Пусть – a £ x £ a, ¦(x) = 0.

При этом исходная система имеет вид:

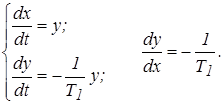(25)

Решение этого уравнения имеет вид , т.е. наклон фазовых траекторий всюду постоянный (отрицательный).

Определим равновесное состояние системы из условия:

(26)

Это условие выполняется при y = 0, т.е. точка вырождается в прямую линию y = 0 на интервале [– а, а]. Фазовые траектории на участке – а< x < a представляют собой прямые с коэффициентом наклона -1/Т₁ при различных значениях начальных условий.

На прямых линиях проставляем стрелки таким образом, чтобы конечное движение стремилось к началу координат.

Пусть х > a, . При этом исходная система нелинейных уравнений имеет вид

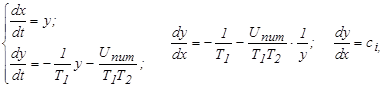(27)

где c_i - семейство изоклин, которое представляет собой прямые параллельные оси х, т.е. , где определяется из выражения для

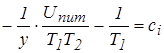. (28)