Реферат: Методы исследования нелинейных систем

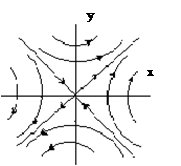
Это уравнение семейства гипербол при изменении A (рис 5).

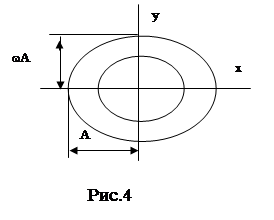Рис. 5

Особая точка называется "седло". Уравнения асимптот (сепаратрис) при А = 0 имеют вид:

3. Пусть корни характеристического уравнения (3) имеют вид

(11)

Фазовая траектория имеет вид сворачивающейся спирали (рис. 6), а точка равновесия называется "устойчивый фокус".

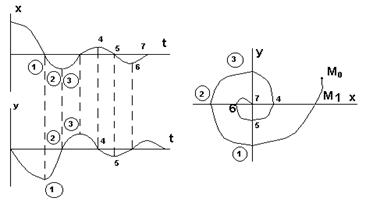
Рис. 6

4. Пусть корни характеристического уравнения (3) имеют вид

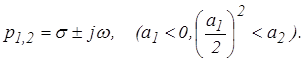(12)

Переходный процесс представляет собой расходящиеся колебания, фазовая траектория – разворачивающаяся спираль. Особая точка называется "неустойчивый фокус" (рис. 7).

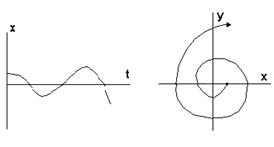
Рис. 7

5. Пусть корни характеристического уравнения (3) имеют вид

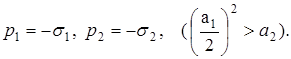(13)

Переходный процесс имеет апериодический характер. Особая точка называется "устойчивый узел" (рис. 8).

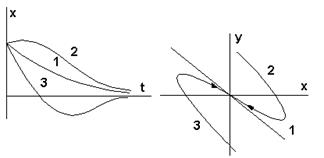
Рис. 8

6. Пусть корни характеристического уравнения (3) имеют вид

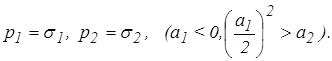(14)

Особая точка называется "неустойчивый узел" (рис. 9).

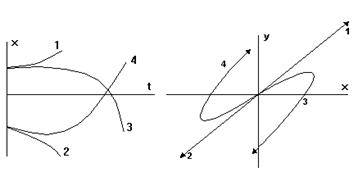
Рис. 9

4. Методы построения фазовых портретов

Для построения фазовых портретов можно использовать различные методы: метод дифференциальных уравнений, метод изоклин, и др.

Метод дифференциальных уравнений . Сущность метода заключается в том, что по дифференциальным уравнениям отдельных участков нелинейного элемента строят соответствующие фазовые портреты на плоскости.

Метод изоклин – это метод линий постоянного наклона.

Пусть даны уравнения нелинейной системы:

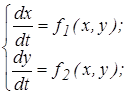(15)