Реферат: Методы исследования нелинейных систем

1. Метод дифференциальных уравнений

Дифференциальное уравнение замкнутой нелинейной системы n-го порядка (рис. 1) можно преобразовать к системе n-дифференциальных уравнений первого порядка в виде:

где: – переменные, характеризующие поведение системы (одна из них может быть регулируемая величина); – нелинейные функции; u – задающее воздействие.

Обычно, эти уравнения записываются в конечных разностях:

,

где – начальные условия.

Если отклонения не большие, то эту систему можно решать, как систему алгебраических уравнений. Решение можно представить графически.

2. Метод фазового пространства

Рассмотрим случай, когда внешнее воздействие равно нулю (U = 0).

Движение системы определяется изменением ее координат - в функции времени. Значения в любой момент времени характеризует состояние (фазу) системы и определяет координаты системы имеющей n – осей и могут быть представлены как координаты некоторой (изображающей) точки М (рис. 2).

Фазовым пространством называется пространство координат системы.

С изменением времени t точка М движется по траектории, называемой фазовой траекторией . Если менять начальные условия получим семейство фазовых траекторий, называемых фазовым портретом . Фазовый портрет определяет характер переходного процесса в нелинейной системе. Фазовый портрет имеет особые точки, к которым стремятся или от которых уходят фазовые траектории системы (их может быть несколько).

Рис. 2

Фазовый портрет может содержать замкнутые фазовые траектории, которые называются предельными циклами. Предельные циклы характеризуют автоколебания в системе. Фазовые траектории нигде не пересекаются, кроме особых точек, характеризующих равновесные состояния системы. Предельные циклы и состояния равновесия могут быть устойчивыми или не устойчивыми.

Фазовый портрет полностью характеризует нелинейную систему. Характерной особенностью нелинейных систем является наличие различных типов движений, нескольких состояний равновесия, наличие предельных циклов.

Метод фазового пространства является фундаментальным методом исследования нелинейных систем. Исследовать нелинейных систем на фазовой плоскости гораздо проще и удобнее, чем с помощью построения графиков переходных процессов во временной области.

Геометрические построения в пространстве менее наглядны, чем построения на плоскости, когда система имеет второй порядок, при этом применяется метод фазовой плоскости.

Применение метода фазовой плоскости для линейных систем

Проанализируем связь между характером переходного процесса и кривыми фазовых траекторий. Фазовые траектории могут быть получены либо путем интегрирования уравнения фазовой траектории, либо путем решения исходного дифференциального уравнения 2-го порядка.

Пусть задана система (рис. 3).

Рассмотрим свободное движение системы. Приэтом: U(t)=0, e(t)=– x(t)

В общем виде дифференциальное уравнение имеет вид

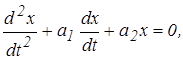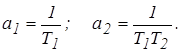где (1)

Это однородное дифференциальное уравнение 2-го порядка его характеристическое уравнение равно

. (2)

Корни характеристического уравнения определяются из соотношений

--> ЧИТАТЬ ПОЛНОСТЬЮ <--