Реферат: Методы обучения математике в 10 -11 класах
(-;0)(4;)
Точки:
максимуму
мінімуму
, для х(-;-1)
, для х(1; )
х = 4
нема
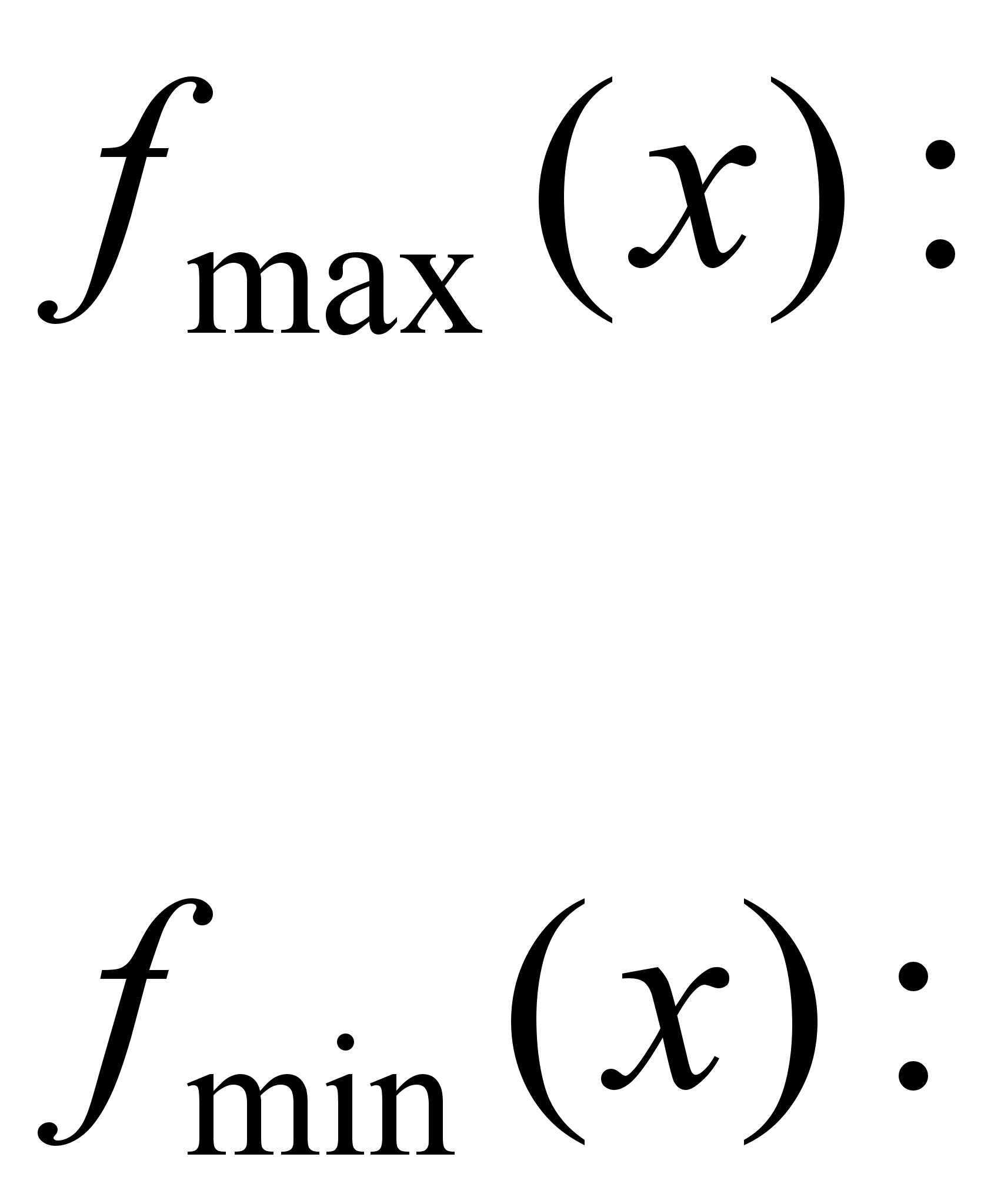
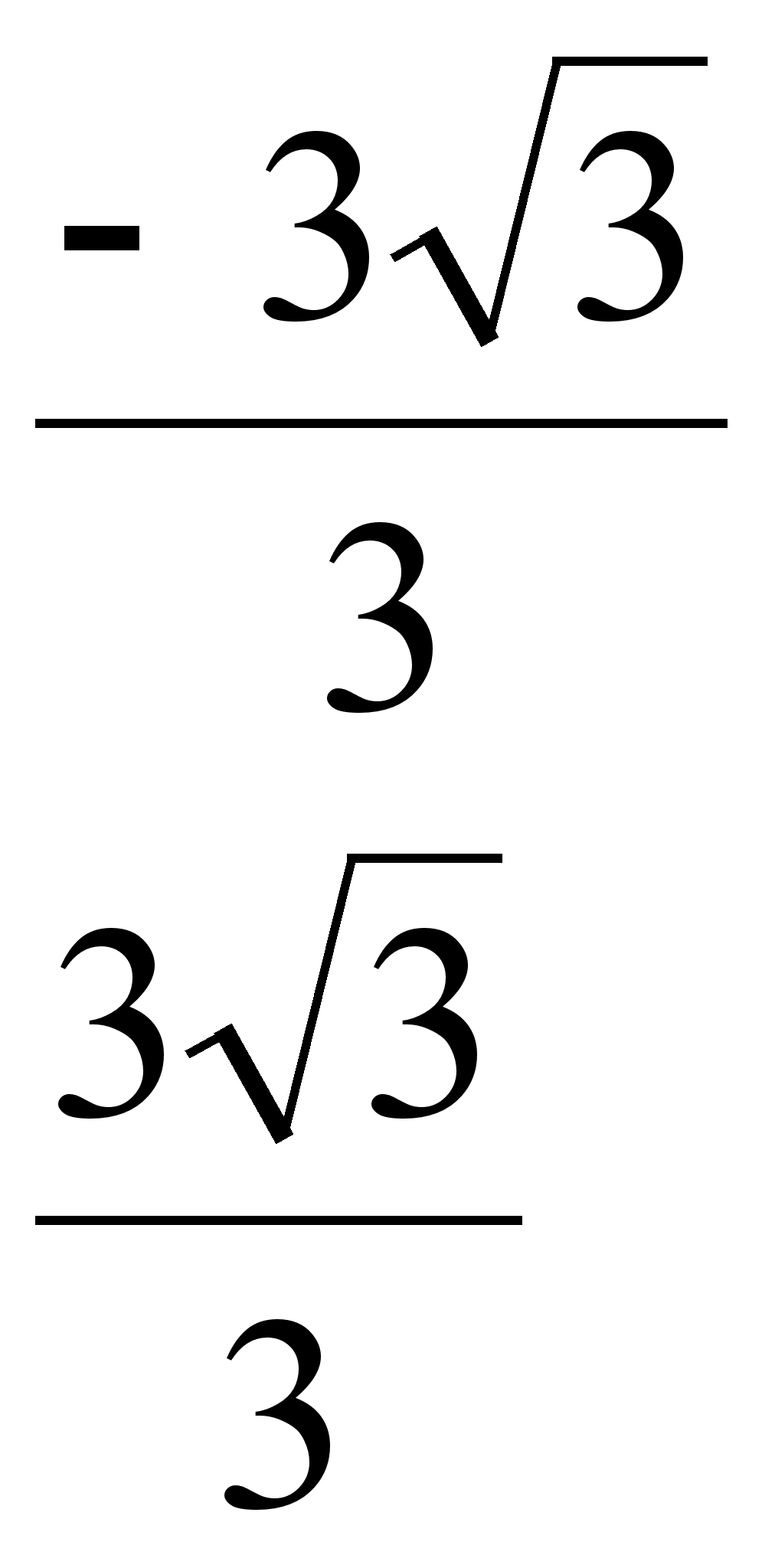
нема
Потім учні самостійно будують графік другої функції (мал. 9*).
Після пояснення вчителем теоретичного матеріалу і наведення декількох прикладів дослідження функції учні вже самі досліджують і будують графіки функцій.
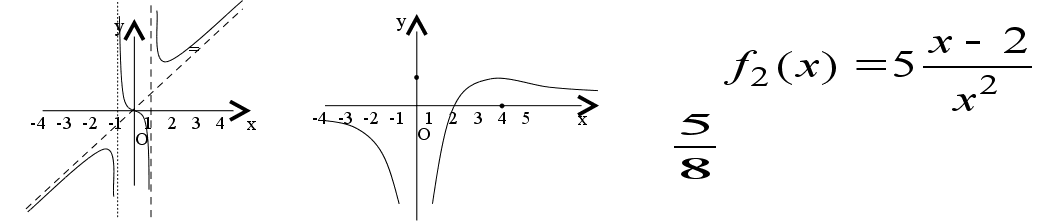
Мал. 9 Мал. 9*
§3. ПРОБЛЕМНИЙ ВИКЛАД
При вивченні теми “Застосування похідної в фізиці та техніці” урок починається з пригадування того, яким чином визначається швидкість руху в курсі фізики. Розглянемо випадок, коли матеріальна точка рухається по координатній прямій, і задано закон руху цієї точки, тобто координата х цієї точки є відома функція 
часу 
. За момент часу від 
до 
переміщення точки можемо записати як 
= =
, а середня швидкість руху точки 
.
При 
значення середньої швидкості прямує до конкретного значення, яке називають миттєвою швидкістю 
матеріальної точки в момент часу . Тобто 
при .
За означенням похідної 
при .
Вважають, що миттєва швидкість 
визначена тільки для диференційованої функції , тому 
.
Скорочено це говорять наступним чином: похідна від координати за часом є швидкість. Це механічний зміст похідної. Миттєва швидкість може приймати довільні значення.
Аналогічно кажуть про зміну швидкості: похідна від швидкості за часом є прискорення. 
.
Тепер розглядаються приклади.
Приклад 1. Розглянемо вільне падіння матеріальної точки.
З фізики відомо, що при вертикальному падінні рух тіла задається формулою 
. Відшукаємо швидкість падіння точки в момент часу : 
. Відшукаємо прискорення падіння точки: 
, прискорення є величина постійна.
Приклад 2.Нехай залежність координати точки, що рухається по прямій, від часу виражена формулою: 
, де 
, 
- константи. Відшукаємо швидкість і прискорення руху.
Швидкість руху буде: 
.
Так як нам відома швидкість руху як функція часу, то можемо знайти прискорення цього руху: 
. Бачимо що а – константа, і при а > 0 – це буде прискорений рух, а при а < 0 – рух сповільнений.
Приклад 3. Судно В знаходиться на сході від судна А на відстані
75 км і пливе на захід зі швидкістю 12 км/год. Судно А пливе на південь зі швидкістю 4 км/год. Чи буде в деякий момент часу відстань між ними мінімальною?
Розв’язання
Перш за все необхідно намалювати малюнок.