Реферат: Методы обучения математике в 10 -11 класах
![]()
![]()
З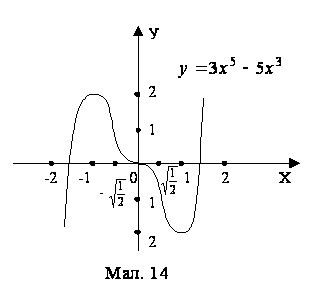 таблиці видно, що функція має максимум в точці
таблиці видно, що функція має максимум в точці ![]() і мінімум в точці
і мінімум в точці ![]() .
.
Будуємо сам графік використовуючи отримані дані з таблиці. Спочатку учні відмічають на графіку точки максимуму і мінімуму, точки перетину з осями, а потім будують графік даної функції.
Приклад2.За даним рівнянням руху авто ![]() знайти його швидкість (при t = 2 сек.) ; момент часу, коли авто почало рухатись в зворотному напрямку та відстань, на яку воно відійшло від деякого пункту (початок руху) до розвороту.
знайти його швидкість (при t = 2 сек.) ; момент часу, коли авто почало рухатись в зворотному напрямку та відстань, на яку воно відійшло від деякого пункту (початок руху) до розвороту.
Розв’язання
Бажано спочатку намалювати графік руху авто, це спростить розв’язування задачі, та дасть можливість зрозуміти, яким чином рухалось авто.
З умови задачі видно, що ![]() .
.
Знаходимо точки перетину графіка функції ![]() з віссю ОХ: t3 - 4t = 0;
з віссю ОХ: t3 - 4t = 0;
t = 0, t = ± 2. (t = -2 не розглядаємо, бо час t >0).
Знаходимо точки екстремуму функції: ![]() ; 3t 2 – 4 = 0; t =
; 3t 2 – 4 = 0; t =![]() .
.
Значення ![]() - не задовольняє умові
- не задовольняє умові ![]() . Перевіримо як змінює знак похідна при переході через точку
. Перевіримо як змінює знак похідна при переході через точку 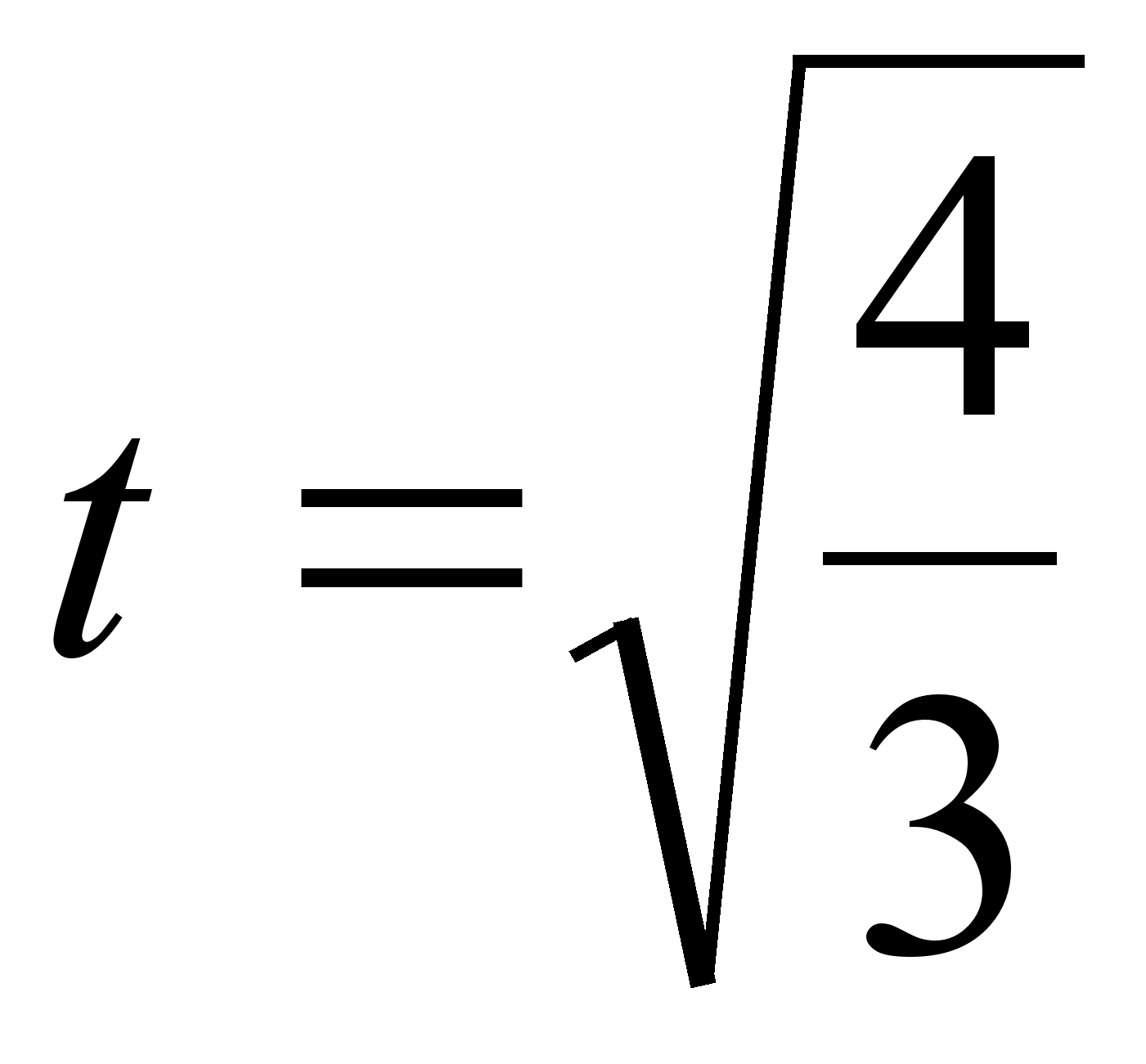 .
.
При переході через цю точку, похідна змінює свій знак з “–” на “+”, тобто це точка мінімуму.
М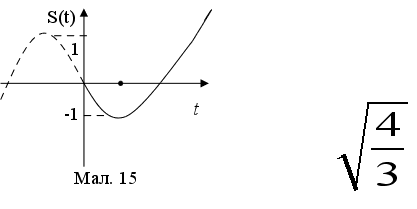 алюємо малюнок.
алюємо малюнок.
З малюнку видно, що в момент часу t =![]() авто знаходилось на максимальній відстані від деякого пункту (хоч і рухалося в зворотному напрямку).
авто знаходилось на максимальній відстані від деякого пункту (хоч і рухалося в зворотному напрямку).
Тому в момент часу t =![]() авто змінило напрям руху.
авто змінило напрям руху.
Відстань в цей момент була: 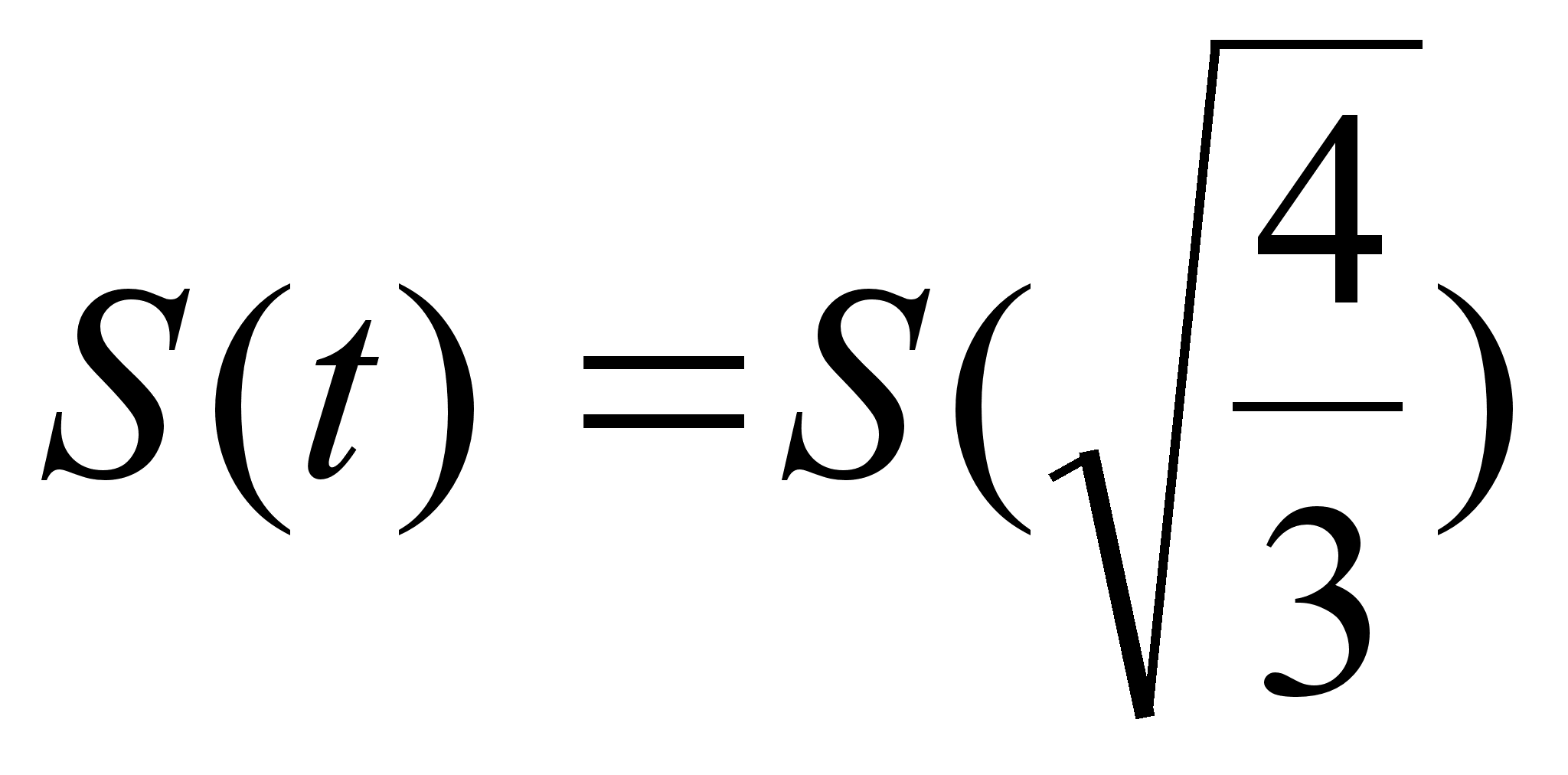 =
=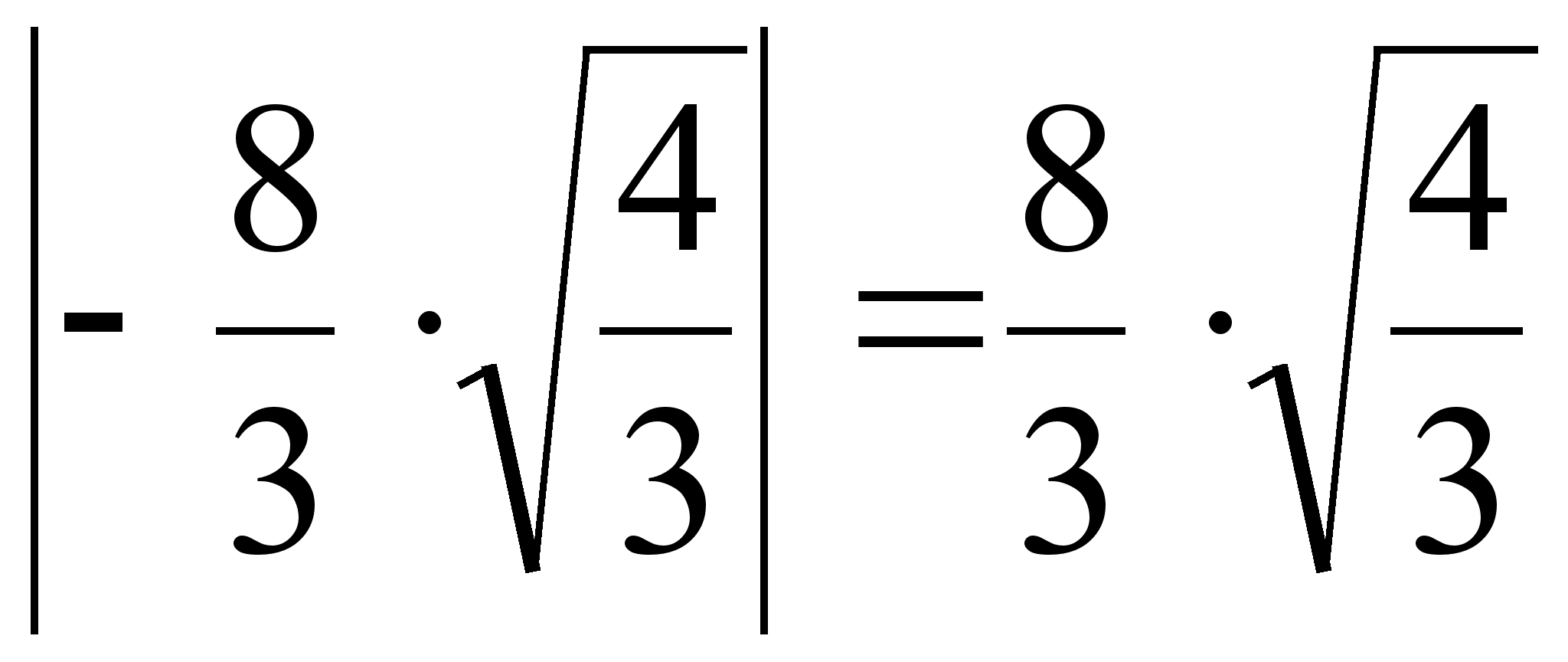 .
.
(стоїть модуль, бо відстань повинна бути додатна).
Похідна від відстані це є швидкість, яку ми вже знайшли: ![]()
![]() , тому через 2 секунди після початку руху авто мало швидкість
, тому через 2 секунди після початку руху авто мало швидкість ![]()
![]() м/с.
м/с.
§6 . МЕТОД ДОЦІЛЬНИХ ЗАДАЧ
В багатьох випадках , в певних темах цей метод застосовується не дуже часто, але при продовженні деякої теми, чи при вивченні теми з розв’язання практичних задач краще скористатися ним, тоді в учнів при вивченні теми буде повніше розуміння вивченого матеріалу. Як вже було вище сказано, суть методу в тому, що розгляд нової теми розпочинається з наведення деяких прикладів, що можуть допомогти учням краще орієнтуватися в тому, про що йде мова в даній темі, або протягом уроку посилатися на деякі з них.
Розглянемо його використання на прикладі вивчення теми “Функції та їх графіки”.
Вчитель на початку уроку, але вже після означення поняття функції, може наводити приклади, будувати з учнями графіки, а потім на основі графіків вивести певні закономірності їх побудови і запропонувати учням використовувати ці закономірності при подальшому розв’язуванні прикладів.
П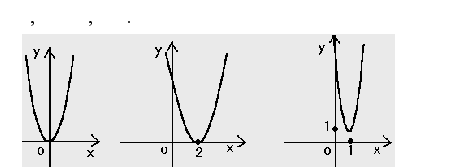 обудуємо графіки таких елементарних функцій:
обудуємо графіки таких елементарних функцій:
Мал. 16 Мал. 17 Мал.18
Учні помічають, що другий графік (Мал. 17.) зсунутий на 2 одиниці вправо, а в формулі стоїть знак мінус перед цією цифрою. Третій графік (Мал. 18.) відрізняється від другого тим, що не тільки зсунутий по осі OX, а й по осі OY – на 1, але тут вже спостерігається відповідність знаку.
Після розглядання цих прикладів учні можуть сформулювати основні правила побудови графіків не тільки степеневих функцій, а і графіків довільних функцій.
Запишемо загальний вигляд функції: ![]() (
(![]() ,
, ![]() ).
).
Для побудови графіку довільної степеневої функції необхідно:
-
побудувати графік функції
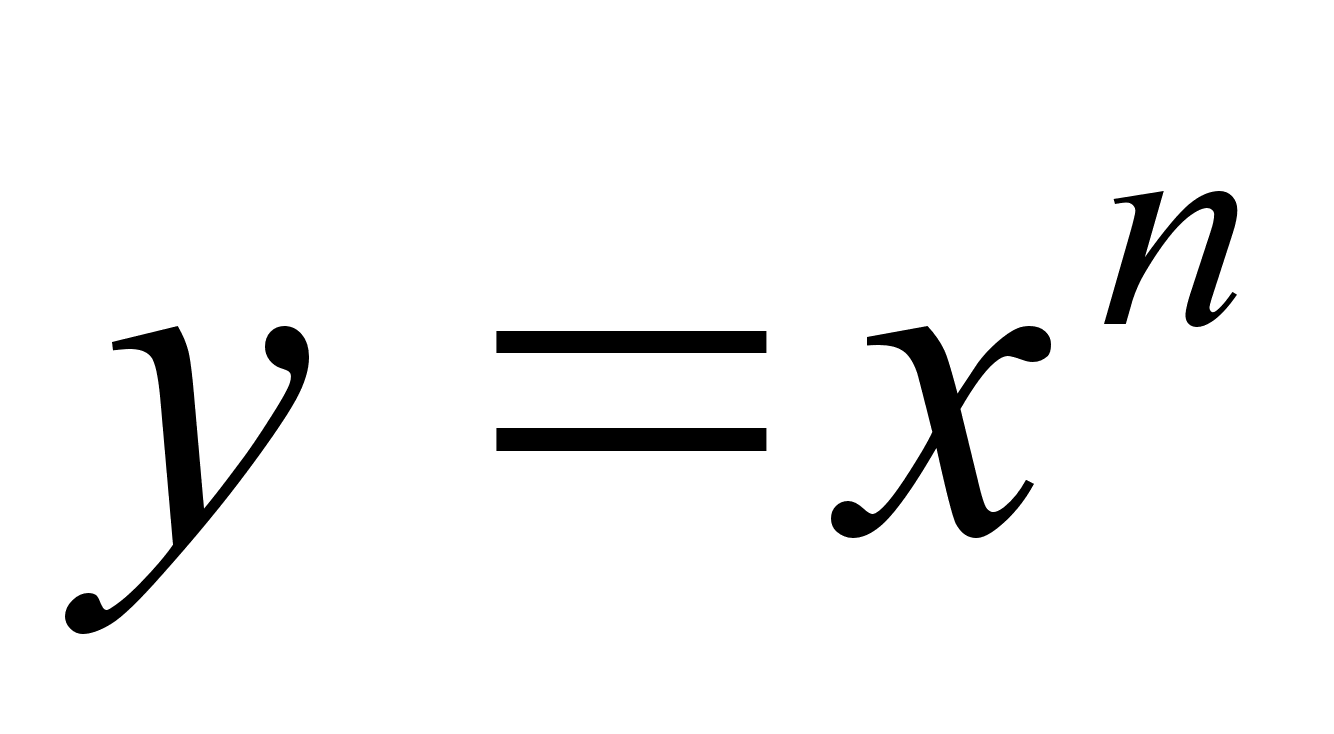 ;
;