Реферат: Методы решения некорректно поставленных задач

Если М — компакт, то квазирешение, очевидно, существу­ет для любого и ÎU и если, кроме того, и ÎAM, то ква­зирешение z¹ совпадает с обычным (точным) решением уравнения (2; 0,1). Квазирешение может быть и не одно. В этом случае под квазирешенпем будем разуметь любой элемент из множества квазирешенийD.

Можно указать достаточные условия, при которых квазирешение единственно и непрерывно зависит от пра­вой части и.

Напомним определение. Пусть элемент у и множество Q принадлежат пространству U. Элементq множестваQ называется проекцией элемента у на множество Q, q =Ру, если выполняется равенство

где

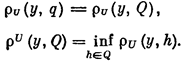
Теорема 1. Если уравнение Аz= u может иметь на компакте М не болееодного решения и проекция каждого элемента uÎU на множество N = AM единственна, то квазирешение уравнения (2; 0,1) единственно и непре­рывно зависит от правой части u.

Доказательство. Пусть z¹ — квазирешение и и ¹ =А z¹ . Очевидно, и ¹ есть проекция элемента u на множе­ство N =AM. По условию теоремы она определяется од­нозначно. Отсюда, в силу взаимной однозначности ото­бражения множества М на множествоN, следует един­ственность квазирешения z¹ .

Очевидно, что z¹ = А^-1 u=А ^-1 Ри. Согласно лемме о непрерывности обратного отображения компакта (см. предыдущий параграф) оператор А^-1 непрерывен на N. Оператор проектирования Р непрерывен на U. Поэтому А^-1 P — непрерывный на U оператор и, следовательно, квазирешение z¹ непрерывно зависит от правой части и.

Таким образом, при переходе к квазирешению восста­навливаются все условия корректности, т. е. задача на­хождения квазирешения уравнения (2; 0,1) на компакте М является корректно поставленной.

Если условие единственности решения уравнения (2; 0,1) не выполнено, то квазирешения образуют некото­рое множествоD элементов компакта М. В этом случае без упомянутых в теореме 1 ограничений на множество N имеет место непрерывная зависимость множества квази­решений D от и в смысле непрерывности многозначных отображений. Для случая, когда уравнение (2; 0,1) линейно, легко получить более общие результаты, содержащиеся в сле­дующей теореме .

Теорема 2.Пусть уравнение (2; 0,1) линейно, одно­родное уравнение Az=0имеет только нулевое решение, множество М выпукло, а всякая сфера в пространстве U строго выпукла. Тогда квазирешение уравнения (2; 0,1) на компакте М единственно и непрерывно зависит от пра­вой части и.

Доказательство. Пусть z¹ — квазирешение и u¹ =Az¹ . Так как множество М выпукло, то в силу линей­ности оператора А множество N =AM также выпукло. Очевидно, что и ¹ есть проекция элемента и на множество N. В силу того, что сфера в пространстве U по условию теоремы строго выпукла, проекция и определяется одно­значно. Далее доказательство завершается, как в тео­реме 1.

2.2.3. ПустьF и U — гильбертовы пространства, М ÎS_R — шар (|| z ||<=R ) в пространстве F и А — вполне непре­рывный линейный оператор.

В этом случае квазирешение уравнения (2; 0,1) мож­но представить в виде ряда по собственным элементам (функциям, векторам) j_n оператора А*А, где А* — опе­ратор, сопряженный оператору А.

Известно, что А*А — самосопряженный положитель­ный вполне непрерывный оператор из F в F. Пусть l₁ >=l₂ >=…>=l_n >=… — полная система его собственных значений, a j₁ , j₂ ,…, j_n ,…—отвечающая им полная ортонормированная система его собственных элементов (функций, векторов). Элемент А*и можно представить в виде ряда

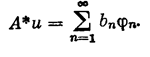(2;2,2)

В этих условиях справедлива

Теорема 3. Квазирешение уравнения (2, 0,1) намножествеS_R выражается формулами:

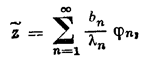(2;2,3)

если

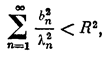(2;2,4)

и

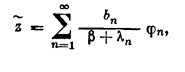
если

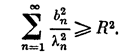(2;2,5)

Здесьb —корень уравнения

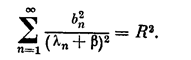(2;2,6)

Доказательство. Квазирсшение минимизирует функционал

r_U ² (Az,u) == (Az —u, Az — u) (2;2,7)

(где (v,w ) — скалярное произведение элементовv иw из U), уравнение Эйлера для которого имеет вид

A*Az=A*u. (2;2,8)

Решение этого уравнения будем искать в виде ряда по системе {j_n }:

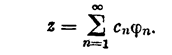(2;2,9)

Подставляя этот ряд в уравнение (2; 2,8) и используя разложение (2;2,2), находим с_n =b_n / l_n . Следователь­но, неравенство (2; 2,4) означает, что ||z||<R и речь идет о нахождении безусловного экстремума функциона­ла (2; 2,7). Ряд (2; 2,3) и будет решением задачи.

Если же выполняется неравенство (2; 2,5), то это означает, что ||z||>=R и надо решать задачу на услов­ные экстремум функционала (2; 2,7) при условии, что || z ||² =R² . Методом неопределенных множителей Лагранжа эта задача сводится к нахождению безусловного экстремума функционала