Реферат: Многочлены Лежандра, Чебышева и Лапласа
СОДЕРЖАНИЕ
Введение
1. Многочлены Лежандра
2. Многочлены Чебышева
3. Преобразование Лапласа
4. Обращение преобразования Лапласа с помощью многочленов, ортогональных на конечном промежутке
4.1 Постановка задачи
4.2.Обращение преобразования Лапласа с помощью смещенных многочленов Лежандра
4.3. Обращение преобразования Лапласа с помощью смещенных многочленов Чебышева первого рода.
Заключение
преобразование смещенный многочлен исчисление
ВВЕДЕНИЕ
Математический анализ – раздел математики, дающий методы количественного исследования разных процессов изменения; занимается изучением скорости изменения (дифференциальное исчисление) и определением длин кривых, площадей и объемов фигур, ограниченных кривыми контурами и поверхностями (интегральное исчисление). Для задач математического анализа характерно, что их решение связано с понятием предела.
Начало математическому анализу положил в 1665 И.Ньютон и (около 1675) независимо от него Г.Лейбниц, хотя важную подготовительную работу провели И.Кеплер (1571–1630), Ф.Кавальери (1598–1647), П.Ферма (1601–1665), Дж.Валлис (1616–1703) и И.Барроу (1630–1677).
Операционное исчисление –раздел математики, занимающийся главным образом алгебраическими операциями, производимыми над символами операции (или преобразования).
Во многих задачах математического анализа рассматриваются ситуации, в которых каждая точка одного пространства ставится в соответствие некоторой точке другого (или того же) пространства. Пространства могут быть абстрактными, в которых «точки» в действительности являются функциями. Соответствие между двумя точками устанавливается с помощью преобразования или оператора. В задачу теории операторов входит подробное описание и классификация различных видов преобразований и их свойств, а также разработка символических методов, позволяющих минимизировать и упростить вычисления. Обычно теорию операторов применяют к пространствам, в которых допускается сложение или умножение точек, т.е. линейным пространствам, группам, кольцам, полям и т.д.
Операционное исчисление позволяет осуществить абстрактные постановки задач и обобщить такие разделы математического анализа, как теория дифференциальных и интегральных уравнений. Мощным стимулом для развития теории операторов стали современные проблемы квантовой теории. Наиболее полные результаты получены для дистрибутивных операторов в т.н. гильбертовом пространстве. Интерес к этой области во многом связан с представлением таких операторов интегральными преобразованиями.
В середине XIX века появился ряд сочинений, посвящённых так называемому символическому исчислению и применению его к решению некоторых типов линейных дифференциальных уравнений. Сущность символического исчисления состоит в том, что вводятся в рассмотрение и надлежащим образом интерпретируются функции оператора дифференцирования.
![]() .
.
Среди сочинений по символическому исчислению следует отметить вышедшую в 1862 году в Киеве обстоятельную монографию русского математика М. Е. Ващенко-Захарченко «Символическое исчисление и приложение его к интегрированию линейных дифференциальных уравнений». В ней поставлены и разрешены основные задачи того метода, который в дальнейшем получил название операционного.
В 1892 году появились работы английского учёного О. Хевисайда, посвящённые применению метода символического исчисления к решению задач по теории распространения электрических колебаний в проводах.
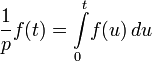
В отличие от своих предшественников, Хевисайд определил обратный оператор однозначно, полагая и считая f (u ) = 0 для u < 0. Труды Хевисайда положили начало систематическому применению символического, или операционного, исчисления к решению физических и технических задач.

Однако широко развитое в трудах Хевисайда операционное исчисление не получило математического обоснования, и многие его результаты оставались недоказанными. Строгое обоснование было дано значительно позже, когда была установлена связь между функциональным преобразованием Лапласа и оператором дифференцирования
![]()
если существует производная ![]() , для которой
, для которой
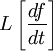
существует и f (0) = 0, то
--> ЧИТАТЬ ПОЛНОСТЬЮ <--