3.2. Вывод дифференциального уравнения теплопроводности. 17

4 СОСТАВЛЕНИЕ АЛГОРИТМА.. 20

5 СОСТАВЛЕНИЕ ПРОГРАММЫ... 22

6 АНАЛИЗ МОДЕЛИРОВАНИЯ И РАСЧЁТОВ.. 24

СПИСОК ИСПОЛЬЗОВАНОЙ ЛИТЕРАТУРЫ... 25

ПРИЛОЖЕНИЕ1. 26

ПРИЛОЖЕНИЕ2. 27

ВВЕДЕНИЕ

Переработка полимерных материалов — это совокупность техноло­гических приемов, методов и процессов, посредством которых ис­ходный полимер превращают в различные изделия с заданными эксплуатационными характеристиками.

Полимеры начали перерабатывать в конце XIX в., а к сере­дине XX в. переработка полимеров выделилась в самостоятельную область техники, в которой используется специализированное вы­сокопроизводительное оборудование, необходимое для реализации в промышленных масштабах специфических для полимеров техно­логических процессов.

Вследствие большой производительности современного перера­батывающего оборудования и высокой стоимости технологических линий проведение экспериментальных исследований реального про­цесса переработки полимеров, даже осуществленных с примене­нием современных методов экстремального планирования, пре­вращается в дорогостоящую и продолжительную работу. Поэтому целесообразно изучать особенность каждого конкретного процесса, рассматривая вначале его теоретическое описание, т. е. его мате­матическую модель.

При таком подходе в каждом конкретном случае этапу физи­ческого эксперимента (будь то создание несложной установки, конструирование технологической линии или опробование нового технологического режима) всегда предшествует этап теоретиче­ского эксперимента. На этом этапе нет необходимости прибегать к реальным экспериментам, вместо этого исследуются количествен­ные характеристики процесса, полученные расчетным методом.

Такой подход позволяет существенно снизить объем физиче­ского эксперимента, поскольку прибегать к нему приходится на самой последней стадии — не в процессе поиска основных законо­мерностей, адля проверки и уточнения выданных рекомендаций. Разумеется, для того чтобы исследуемые теоретические модели процессов описывали эти процессы с достаточно хорошим прибли­жением, они непременно должны учитывать основные особенно­сти моделируемых явлении.

При математическом описании реальных производственных процессов приходится прибегать к существенным упрощениям. При этом значительную помощь в создании математических моделей оказывает анализ простых слу­чаев. Прием такого рода вполне допустим, он позволяет независимо устанавливать основные закономерности наиболее простых случаев выбранных в качестве математического аналога поведения полимерных расплавов.

Термодинамические соотношения, описывающие разогрев и плавление полимеров, являются фундаментом, на базе которого строятся неизотермические модели реальных процессов перера­ботки. Основные вопросы термодинамики и теплопередачи в поли­мерах рассмотрены в данной работе.

1. АНАЛИЗ ИСХОДНЫХ ДАННЫХ

1.1 Неограниченный цилиндр.

Рассмотрим неограниченный цилиндр радиуса R, температура поверхности которого остается неизменной на протяжении всего процесса теплообмена. Радиальное распределение температур в начальный момент задано в виде некоторой функции Т(r). Необходимо найти распределение температур. Такие задачи встречаются при расчете процессов охлаждения полимерного волокна, затвердевания литников литьевых форм и т. п.

Дифференциальное уравнение теплопроводности для цилиндра имеет вид:

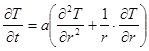(1.1)

Краевые условия: (1.2)

(1.3)

(1.4)

Решение, полученное методом разделения переменных, имеет сложный вид потому задачей данной работы является найти численное его решение.

1.2 Описание переменных

Уравнение теплопроводности устанавливает зависимость между следующими величинами характеризующими процесс теплопроводности:

T-температура по Цельсию (градус)

r-радиус цилиндра (М)

t-время (С)

a-коэффициент температуропроводности (градус/с*м2)

2 1.3 Граничные условия

Для решения данного дифференциального уравнения в частных производных необходимыми данными является значения производных температуры по радиусу на оси цилиндра, которая должна быть равной нулю (1.4).

Температуру стенки цилиндра, через которую происходит охлаждение литника примем равной 30 градусов.

(1.5)

Радиус литника обычно составляет 0.01 м.

R=0.01 (1.6)

Распределение температуры в начальный момент времени по радиусу задано в виде убывающей экспоненциальной функции, чтобы производная температуры по